
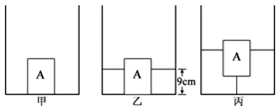
 如图甲所示,一个不计外壁厚度且足够高的柱形容器放在水平桌面上,容器中立放着一个底面积为100cm2、高为12cm均匀实心长方体木块A,A的底部与容器底用一根细绳连在一起.现慢慢向容器中加水,当加入1.8kg的水时,木块A对容器底部的压力刚好为0,如图乙所示,此时容器中水的深度为9cm.已知细绳长度为L=8cm,ρ水=1.0×103kg/m3),求:
如图甲所示,一个不计外壁厚度且足够高的柱形容器放在水平桌面上,容器中立放着一个底面积为100cm2、高为12cm均匀实心长方体木块A,A的底部与容器底用一根细绳连在一起.现慢慢向容器中加水,当加入1.8kg的水时,木块A对容器底部的压力刚好为0,如图乙所示,此时容器中水的深度为9cm.已知细绳长度为L=8cm,ρ水=1.0×103kg/m3),求:分析 (1)根据木块A底面积和水的深度,可求木块A排开水的体积,再利用阿基米德原理求物块受到的浮力;
(2)由于木块A对容器底部的压力刚好为0,则重力与浮力相等;利用G=mg求木块的质量,再利用密度公式求木块的密度;
(3)根据水的体积求出木块A浸入水的体积,进一步求细绳剪断前、剪断后排开水的体积变化,知道容器底面积,可求水深的变化量,再利用液体压强公式求容器底所受压强改变量;
(4)根据阿基米德原理求出A刚好沉没时受到的浮力大小,与A的重力比较,根据A处于静止状态,受平衡力,求出弹簧的拉力作用,根据已知条件求出弹簧的伸长,从而得出弹簧的长度,分别求出A底面以下和以上水的体积,根据m=ρV求加水的质量.
解答 (1)已知木块A的底面积S木=100cm2,
由乙图可知:当木块A对容器底部的压力刚好为0,水的深度为h水=9cm;
则木块A排开水的体积:
V排=S木h水=100cm2×9cm=900m3=9×10-4m3,
木块受到的浮力:
F浮=ρ水V排g=1×103kg/m3×9×10-4m3×10N/kg=9N;
(2)木块A的体积:V木=S木h木=100cm2×12cm=1200cm3=1.2×10-3m3,
由于木块A对容器底部的压力刚好为0,木块A处于漂浮,则G=F浮=9N,
由G=mg=ρVg可得木块的密度:
ρ木=$\frac{{G}_{木}}{{V}_{木}g}$=$\frac{9N}{1.2×1{0}^{-3}{m}^{3}×10N/kg}$=0.75×103kg/m3;
(3)木块A对容器底部的压力刚好为0时,由ρ=$\frac{m}{V}$可得所加水的体积为:
V水1=$\frac{{m}_{水1}}{{ρ}_{水}}$=$\frac{1.8kg}{1×1{0}^{3}kg/{m}^{3}}$=1.8×10-3m3=1800cm3;
由乙图可知:V水1=(S容-S木)h水,(其中h水=9cm)
则容器的底面积为:
S容=$\frac{{V}_{水1}}{{h}_{水}}$+S木=$\frac{1800c{m}^{3}}{9cm}$+100cm2=300cm2;
再次加水后容器中水的总体积为:
V水2=$\frac{{m}_{水2}}{{ρ}_{水}}$=$\frac{4.5kg}{1.0×1{0}^{3}{m}^{3}}$=4.5×10-3m3=4500cm3;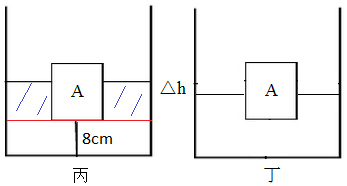
如上图丙中可知,木块下表面以下水的体积(图中红线以下)为:
V1=S容L=300cm2×8cm=2400cm3,
则红线以上水的体积为:
V2=V水2-V1=4500cm3-2400cm3=2100cm3,
设此时木块浸入水的深度为h′,则V2=(S容-S木)h′,
所以,木块浸入水的深度:
h′=$\frac{{V}_{2}}{{S}_{容}{-S}_{木}}$=$\frac{2100c{m}^{3}}{300c{m}^{2}-100c{m}^{2}}$=10.5cm,
此时木块排开水的体积为:
V排′=S木h′=100cm2×10.5cm=1050cm3;
若将细线剪断,木块将上浮,当木块静止时漂浮如上图丁,
由于图丁与图甲中的木块都是漂浮,则木块受到的浮力相等,排开水的体积相等,
所以,细线剪断后木块漂浮时,其排开水的体积为:
V排″=V排=900cm3,
细绳剪断前、剪断后,排开水的体积变化量:
△V排=V排′-V排″=1050cm3-900cm3=150cm3,
则水的深度变化量:
△h═$\frac{△{V}_{排}}{{S}_{容}}$=$\frac{150c{m}^{3}}{300c{m}^{2}}$=0.5cm=5×10-3m,
所以,水对容器底部压强的变化量:
△p=ρ水g△h=1×103kg/m3×10N/kg×5×10-3m=50Pa;
(4)实心长方体木块A刚好浸没时到的浮力:
F浮全=ρ水V排全g=ρ水VAg=1×103kg/m3×12×100×10-6m3×10N/kg=12N;
而A的重力为9N,因浮力大于重力,故弹簧伸长,A受竖直向上的浮力和竖直向下的重力作用及弹簧对A竖直向下的拉力T作用,因此时A处于静止状态,受平衡力的作用,即
GA=F浮全+T;
故弹簧对A的拉力:
T=GA-F浮全+=12N-9N=3N,
因在一定范围内,弹簧受到的拉力每增大1N,弹簧的长度就伸长1cm,故此时弹簧伸长了3cm,故弹簧总长为:
L=8cm+3cm=11cm,
故A下底面以下水的体积:
V3=S容L=300cm2×11cm=3.3×10cm3,
故A下底面以上水的体积:
V4=(S容-SA)h木=(300cm2-100cm2)×12cm=2.4×10cm3,
加水的总体积为:
V=V3+V4=3.3×10cm3+2.4×10cm3=5.7×10cm3,
故从容器中没有水到A刚好浸没,需加水的质量:
m加=ρ水V=1×103kg/m3×5.7×103×10-6m3=5.7kg.
答:(1)A受到的浮力为9N;
(2)木块A的密度为0.75×103kg/m3;
(3)细绳剪断前、剪断后木块静止时,水对容器底部压强的变化量为50Pa.
(4)从容器中没有水稻A刚好浸没,需加5.7kg的水,此时,弹簧拉力为3N.
点评 本题为力学综合题,考查了学生对重力公式、密度公式、液体压强公式、阿基米德原理、物体的漂浮条件、力的合成与弹簧的伸长与拉力的关系的,为压轴题.本题难点在第三问和第四问,能求出水深变化和分析弹簧的状态是本题的关键.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中物理 来源: 题型:计算题
查看答案和解析>>
科目:初中物理 来源: 题型:实验探究题
 运用知识解决问题:
运用知识解决问题:查看答案和解析>>
科目:初中物理 来源: 题型:填空题
查看答案和解析>>
科目:初中物理 来源: 题型:计算题
查看答案和解析>>
科目:初中物理 来源: 题型:选择题
| A. | 同样重的两个铜块甲和乙,甲浸没在水中,乙浸没在煤油中,甲受到的浮力大 | |
| B. | 同样重的铝块和铜块,都浸没在煤油中,铝块受到的浮力大 | |
| C. | 同样重的铝块和铜块,铜块浸没在煤油中,铝块浸没在水中,铝块受到的浮力大 | |
| D. | 同样重的铝块和铜块,投入到水银中,铜块受到的浮力大 |
查看答案和解析>>
科目:初中物理 来源: 题型:填空题
查看答案和解析>>
科目:初中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com