
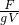 ;
;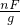 -ρ1V,
-ρ1V,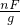 -ρ1V.
-ρ1V.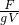 ;
;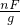 -ρ1V.
-ρ1V.

 阅读快车系列答案
阅读快车系列答案科目:初中物理 来源: 题型:
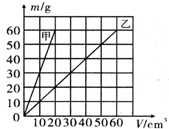 甲、乙两种物质的质量m与体积V的关系如图所示.在水平桌面上竖直放置着由甲、乙两种物质分别制成的相同高度的实心圆柱体,质量比是1:5.那么甲、乙两种物质的密度之比是
甲、乙两种物质的质量m与体积V的关系如图所示.在水平桌面上竖直放置着由甲、乙两种物质分别制成的相同高度的实心圆柱体,质量比是1:5.那么甲、乙两种物质的密度之比是查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
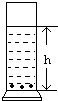 如图所示,在水平桌面上竖直放置一盛有水的容器,在靠近其底部的侧壁上有若干个小孔,水可缓慢地从小孔中渗出,经测试发现:无论容器内水面多高,每隔2分钟水对容器底面的压强总是减小到原来的
如图所示,在水平桌面上竖直放置一盛有水的容器,在靠近其底部的侧壁上有若干个小孔,水可缓慢地从小孔中渗出,经测试发现:无论容器内水面多高,每隔2分钟水对容器底面的压强总是减小到原来的| 9 |
| 10 |
查看答案和解析>>
科目:初中物理 来源:2011-2012学年四川省成都市金堂县广兴中学八年级(下)期末物理模拟试卷(七)(解析版) 题型:选择题

 -ρ1V
-ρ1V
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com