
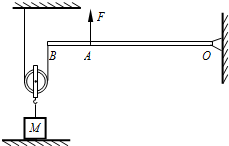
 边长为0.1m质量均匀的正方体物体M,单独放在水平地面上对地面的压强为5.4×103 Pa.如图所示装置,横杆可绕固定点O在竖直平面内转动,系在横杆B 端的细绳绕过动滑轮,动滑轮连着物体M.用力F在A点竖直向上提横杆时,横杆在水平位置平衡,此时物体M 对地面的压强为1.8×103 Pa,若仍用力F在距离A点0.1m处竖直向上提横杆,使横杆仍在水平位置平衡,此时物体M 对地面压强为1.0×103 Pa,已知横杆上AB部分的长为0.2m,AB:OA=1:3,g取10N/kg,不计横杆质量、绳质量和摩擦.则力F的大小为________N.
边长为0.1m质量均匀的正方体物体M,单独放在水平地面上对地面的压强为5.4×103 Pa.如图所示装置,横杆可绕固定点O在竖直平面内转动,系在横杆B 端的细绳绕过动滑轮,动滑轮连着物体M.用力F在A点竖直向上提横杆时,横杆在水平位置平衡,此时物体M 对地面的压强为1.8×103 Pa,若仍用力F在距离A点0.1m处竖直向上提横杆,使横杆仍在水平位置平衡,此时物体M 对地面压强为1.0×103 Pa,已知横杆上AB部分的长为0.2m,AB:OA=1:3,g取10N/kg,不计横杆质量、绳质量和摩擦.则力F的大小为________N. (F1+G动)
(F1+G动) (F1+G动)×OB=F×OA,
(F1+G动)×OB=F×OA, (36N+G动)×0.8m=F×0.6m-------①
(36N+G动)×0.8m=F×0.6m-------① (F2+G动)
(F2+G动) (F2+G动)×OB=F×OA′,
(F2+G动)×OB=F×OA′, (44N+G动)×0.8m=F×(0.6m+0.1m)-------②
(44N+G动)×0.8m=F×(0.6m+0.1m)-------②

科目:初中物理 来源: 题型:

查看答案和解析>>
科目:初中物理 来源: 题型:
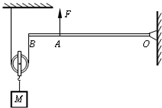 边长为0.1m质量均匀的正方体物体M,放在水平地面上对地面的压强为6.0×103 Pa.用如图所示杠杆和滑轮将物体吊起在空中,杠杆在水平位置平衡时拉力F和B处绳子均垂直杠杆,已知杠杆长OB=0.8m,OA=0.6m,g取10N/kg,不计杠杆、绳及滑轮质量和摩擦.
边长为0.1m质量均匀的正方体物体M,放在水平地面上对地面的压强为6.0×103 Pa.用如图所示杠杆和滑轮将物体吊起在空中,杠杆在水平位置平衡时拉力F和B处绳子均垂直杠杆,已知杠杆长OB=0.8m,OA=0.6m,g取10N/kg,不计杠杆、绳及滑轮质量和摩擦.查看答案和解析>>
科目:初中物理 来源: 题型:解答题
 边长为0.1m质量均匀的正方体物体M,放在水平地面上对地面的压强为6.0×103 Pa.用如图所示杠杆和滑轮将物体吊起在空中,杠杆在水平位置平衡时拉力F和B处绳子均垂直杠杆,已知杠杆长OB=0.8m,OA=0.6m,g取10N/kg,不计杠杆、绳及滑轮质量和摩擦.
边长为0.1m质量均匀的正方体物体M,放在水平地面上对地面的压强为6.0×103 Pa.用如图所示杠杆和滑轮将物体吊起在空中,杠杆在水平位置平衡时拉力F和B处绳子均垂直杠杆,已知杠杆长OB=0.8m,OA=0.6m,g取10N/kg,不计杠杆、绳及滑轮质量和摩擦.查看答案和解析>>
科目:初中物理 来源: 题型:解答题

查看答案和解析>>
科目:初中物理 来源:2013年广西南宁市中考物理试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com