在甲、乙两个完全相同的圆柱形容器内装有质量相等的水.现将A、B两个实心物块分别放入甲、乙两个容器中,物块均可浸没且水不溢出容器.已知A、B两物块的密度分别为ρA=3.0×103kg/m3,ρB=1.5×103kg/m3,两物块的质量关系为2mA=mB.A、B两物块的体积分别为VA、VB,A、B两物块浸没在水中所受浮力分别为FA、FB,物块在水中静止时两容器底部对两物块的支持力分别为NA、NB,放入物块前、后,两容器底部受到水的压强增加量分别为△PA、△PB,放入物块后,桌面受到甲、乙两容器的压力增加量分别为△F甲、△F乙.则下列四项判断中正确的是( )
A.4VA=VB,△PA=4△PB
B.ρA=2ρB,FA=2FB
C.NA=NB,△PA=△PB
D.4FA=FB,2△F甲=△F乙
【答案】
分析:(1)已知甲乙物体的密度可求密度之比,根据密度公式结合质量关系求出体积之比,物体完全浸没时排开水的体积和本身的体积相等,根据阿基米德原理求出受到的浮力之比;
(2)因两圆柱体完全相同,根据体积公式求出水深的变化量,根据液体压强公式求出水对容器底部压强的变化量之比;
(3)水平面上物体的压力和自身的重力相等,对桌面压力的变化量等于实心物块的重力,根据以上分析即可得出答案.
解答:解:(1)ρ
A=3.0×10
3kg/m
3,ρ
B=1.5×10
3kg/m
3,
所以ρ
A:ρ
B=3.0×10
3kg/m
3:1.5×10
3kg/m
3=2:1,
∵V=

,
∴

=

=

×
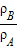
=

×

=

,故A不正确;
∵F
浮=ρgV
排,
∴
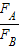
=

=

,故B不正确;
(2)∵物体浸没时,V
排=V,且两容器完全相同的圆柱体,
∴液体深度的变化量△h=
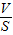
,
∵p=ρgh,
∴

=

=

,故C不正确;
(3)∵水平面上物体的压力和自身的重力相等,且甲乙相同的圆柱形容器内装有质量相等的水,
∴桌面受到的压力的变化量

=

=

,故D正确.
故选D.
点评:本题考查了液体压强和固体压强公式、阿基米德原理、体积公式、密度公式的应用,关键是公式及其变形式的灵活运用,解体时可以利用排除法进行解答,并不一定全部进行解答,这样可以达到事半功倍的效果.

 ,
, =
= =
= ×
×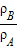 =
= ×
× =
= ,故A不正确;
,故A不正确;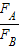 =
= =
= ,故B不正确;
,故B不正确;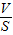 ,
, =
= =
= ,故C不正确;
,故C不正确; =
= =
= ,故D正确.
,故D正确.

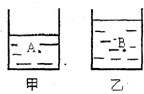 如图所示,在甲、乙两个完全相同的容器中,一个装有500g水,一个装有500g酒精.已知ρ酒精<ρ水,则甲容器中盛的液体是
如图所示,在甲、乙两个完全相同的容器中,一个装有500g水,一个装有500g酒精.已知ρ酒精<ρ水,则甲容器中盛的液体是