
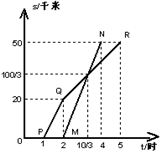
 如图,AB两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,图中PQR和线段MN,分别表示甲和乙所行驶的s与该日下午时间t之间的关系,试根据图形回答:
如图,AB两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,图中PQR和线段MN,分别表示甲和乙所行驶的s与该日下午时间t之间的关系,试根据图形回答: h-2h=
h-2h= h=
h= ×60min=80min;
×60min=80min; km=
km= km;
km;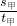 =
=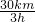 =10km/h;
=10km/h;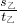 =
=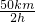 =25km/h.
=25km/h. km;
km; )千米;
)千米; 得出速度;
得出速度; 求得答案.
求得答案.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中物理 来源:2013年安徽省高级中等学校招生考试物理 题型:038
如图,AB两地相距4 km,MN是与AB连线平行的一条小河的河岸,AB到河岸的垂直距离为3 km,小军要从A处走到河岸取水然后送到B处,他先沿垂直于河岸的方向到D点取水然后再沿DB到B处.若小军的速度大小恒为5 km/h,不考虑取水停留的时间.

(1)求小军完成这次取水和送水任务所想要的总时间.
(2)为了找到一条最短路线(即从A到河岸和从河岸到B的总路程最短),可以将MN看成一个平面镜,从A点作出一条光线经MN反射后恰能通过B点,请你证明入射点O即为最短路线的取水点.
查看答案和解析>>
科目:初中物理 来源: 题型:
如图所示,A、B两地相距4 km,MN是与AB![]() 连线平行的一条小河的河岸,AB到河岸的垂直距离为3 km,小明要从A处走到河岸取水,然后送到B处,他先沿着垂直于河岸的方向到D点取水,然后再沿着直线DB到B处,若小明的速度大小恒定为5 km/h,不考虑取水停留的时间。
连线平行的一条小河的河岸,AB到河岸的垂直距离为3 km,小明要从A处走到河岸取水,然后送到B处,他先沿着垂直于河岸的方向到D点取水,然后再沿着直线DB到B处,若小明的速度大小恒定为5 km/h,不考虑取水停留的时间。
(1)求小明完成这次取水和送水任务所需的总时间;
(2)为了找到一条最短路线(即从A到河岸和从河岸到B的总路程最短),可以将MN看成一个平面镜,从A点作出一条光线经MN反射后恰能通过B点,请你作图说明入射点O即为最短的取水点。其他任何一点(如E点或F点)都比该点取水路线要长(保留必要的辅助线)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com