解:(1)因为正方体放在水平地面上,所以F=G=47.04N,
正方体的底面积:S=a
2=(0.2m)
2=0.04m
2,
木块对水平地面的压强:p=
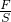
=

=1176Pa;
(2)正方体的体积:V=a
3=(0.2m)
3=0.008m
3,m=
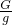
=

=4.8kg,
正方体的密度:ρ=
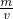
=

=0.6×10
3㎏/m
3;
(3)∵F
浮=G
木,ρ
水gV
浸=m
木g,
∴V
浸=

=

=4.8×10
-3m
3=48cm
3;
(4))∵容器为圆柱形容器,
∴木块对容器底增加的压力:
△F=G
木=47.04N,
∴容器底部受到水的压强增加值:
△p=

=

=196Pa.
(5)由G+F
压=F
浮′得:
竖直向下压力:
F
压=F
浮′-G=ρ
水gV
排′-G=1.0×10
3kg/m
3×9.8N/kg×0.008m
3-47.04N=31.36N.
答:(1)木块对桌面的压强为1176Pa;
(2)木块的密度为0.6×10
3㎏/m
3;
(3)把木块放入底面积为0.24米
2的圆柱形容器里的水中时(容器足够高),木块浸入水中的体积为48cm
3;
(4)木块放入以后水对容器底部压强增加了196Pa;
(5)若要木块A恰能完全浸没在水中,则要在木块上加竖直向下的压力为31.36N.
分析:(1)正方体的重力即为正方体对水平地面的压力,然后算出正方体的底面积,最后就可以根据压强公式算出正方体对水平地面的压强;
(2)先算出正方体的体积和质量,然后根据密度公式就可以算出正方体的密度;
(3)根据木块漂浮,可得出木块受到的浮力,木块浸入水中的体积就是它排开水的体积,再利用浮力的公式即可求出木块浸入水中的体积;
(4)因为是圆柱形容器,放入木块后对容器底增加的压力就是木块的重力,再根据液体压强公式求容器底部受到水的压强增加值;
(5)木块浸没时,排开水的体积等于木块的体积;已知木块排开水的体积和水的密度,利用阿基米德原理可以得到此时木块受到的浮力;已知木块受到的浮力和重力,两者之差就是加上的压力.
点评:本题综合考查了多个公式,包括密度公式、重力公式、压强公式、液体压强公式,关键是知道物体漂浮时浮力等于自身重力以及物体所受外力的分析,分析物体所受外力这是本题的难点也是重点,还要学会浮力公式及其变形的灵活运用.

 有一重为47.04牛,边长为0.2米的实心正方体木块A放在水平桌面上.如图所示,求:
有一重为47.04牛,边长为0.2米的实心正方体木块A放在水平桌面上.如图所示,求: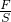 =
= =1176Pa;
=1176Pa;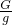 =
= =4.8kg,
=4.8kg,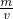 =
= =0.6×103㎏/m3;
=0.6×103㎏/m3; =
= =4.8×10-3m3=48cm3;
=4.8×10-3m3=48cm3; =
= =196Pa.
=196Pa.

 (2009?杨浦区一模)有一重为47.04牛,边长为0.2米的实心正方体木块A放在水平桌面上.如图所示,求:
(2009?杨浦区一模)有一重为47.04牛,边长为0.2米的实心正方体木块A放在水平桌面上.如图所示,求: