有8个盒子中装有电阻,其中一个装有20?的电阻,其余的为10?的电阻.从1号盒里拿1只电阻,从2号盒里拿2只电阻,…,从8号盒里拿8只电阻,串联后得电阻两端电压为10.5伏,通过电流为25毫安.求装有20?的电阻的为几号盒?
解:根据从1号盒里拿1只电阻,从2号盒里拿2只电阻,…,从8号盒里拿8只电阻可知:
电阻的总个数为N=1+2+3+4+5+6+7+8=36,
因串联后得电阻两端电压为10.5伏,通过电流为25毫安,
所以串联后的总电阻为:R=
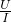
=
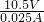
=420Ω,
若8个盒子中取出的全为10?的电阻,则串联后的总阻值为:R′=NR
10=36×10Ω=360Ω,
所以;实际的串联后的电阻值多出的阻值为:△R=R-R′=420Ω-360Ω=60Ω,
则因多出一个20?的电阻,就会增加一个10?,由此可知:
多出的个数为n=
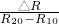
=
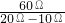
=6;即为6号盒.
答:装有20?的电阻的为6号盒.
分析:利用假设法,若8个盒子中全为10?的电阻,则按上述方式取出组成的电路总电阻值和实际取出的电阻串联的阻值相比较,多出的阻值就是装有20?的电阻引起的,因多出一个20?的电阻,就会增加一个10?,由此可知多出的个数,即为几号盒.
点评:本题考查不同阻值的电阻串联时总阻值的变化判断,本题的难点是通过分析知道从几号盒里拿几只20?的电阻,串联后的总电阻就多出几个10?的电阻.

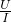 =
=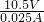 =420Ω,
=420Ω,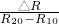 =
=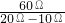 =6;即为6号盒.
=6;即为6号盒.
