
 电烙铁使用前需要一定的预热时间,因而暂时不用也要接在电源上,这样既费电又会造成烙铁头氧化而不易沾锡.小华同学将一把额定电压为220V、额定功率未知的电烙铁与一个小灯泡连接成图所示电路.断开开关S,电烙铁处于预热状态;闭合S,电烙铁很快达到焊接温度.已知灯泡的灯丝在预热状态下电阻为790Ω,经测量,预热时通过电烙铁的电流为0.11A,设电烙铁的电阻不变,电源电压恒为220V,求:
电烙铁使用前需要一定的预热时间,因而暂时不用也要接在电源上,这样既费电又会造成烙铁头氧化而不易沾锡.小华同学将一把额定电压为220V、额定功率未知的电烙铁与一个小灯泡连接成图所示电路.断开开关S,电烙铁处于预热状态;闭合S,电烙铁很快达到焊接温度.已知灯泡的灯丝在预热状态下电阻为790Ω,经测量,预热时通过电烙铁的电流为0.11A,设电烙铁的电阻不变,电源电压恒为220V,求: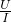 =
=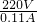 =2000Ω,
=2000Ω,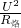 =
=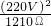 =40W;
=40W;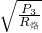 =
= =
= A,
A,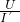 =
=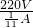 =2420Ω,
=2420Ω, 求出电烙铁的额定功率;
求出电烙铁的额定功率;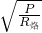 求出预热的功率不超过10W时的最大电流,根据欧姆定律求出电路中的总电阻,再根据电阻的串联特点求出符合要求的最小电阻,据此得出答案.
求出预热的功率不超过10W时的最大电流,根据欧姆定律求出电路中的总电阻,再根据电阻的串联特点求出符合要求的最小电阻,据此得出答案.

科目:初中物理 来源: 题型:
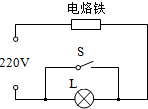 电烙铁使用前需要一定的预热时间,因而若暂时不用也要接在电源上,这样既费电又会造成烙铁头氧化而不易沾锡.小明将一把标有“220V 55W”的电烙铁与一只灯泡(灯丝在预热状态下的电阻为495Ω)连接成如图所示的电路.断开S,电烙铁处于预热状态;闭合S,电烙铁很快达到焊接温度.
电烙铁使用前需要一定的预热时间,因而若暂时不用也要接在电源上,这样既费电又会造成烙铁头氧化而不易沾锡.小明将一把标有“220V 55W”的电烙铁与一只灯泡(灯丝在预热状态下的电阻为495Ω)连接成如图所示的电路.断开S,电烙铁处于预热状态;闭合S,电烙铁很快达到焊接温度.查看答案和解析>>
科目:初中物理 来源: 题型:
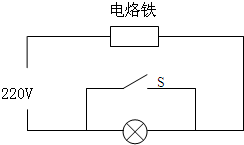 (2007?南充)电烙铁使用前需要一定的预热时间,因而暂时不用也要接在电源上,这样既费电又会造成烙铁头氧化而不易沾锡.小华同学将一把额定电压为220V、额定功率未知的电烙铁与一个小灯泡连接成图所示电路.断开开关S,电烙铁处于预热状态;闭合S,电烙铁很快达到焊接温度.已知灯泡的灯丝在预热状态下电阻为790Ω,经测量,预热时通过电烙铁的电流为0.11A,设电烙铁的电阻不变,电源电压恒为220V,求:
(2007?南充)电烙铁使用前需要一定的预热时间,因而暂时不用也要接在电源上,这样既费电又会造成烙铁头氧化而不易沾锡.小华同学将一把额定电压为220V、额定功率未知的电烙铁与一个小灯泡连接成图所示电路.断开开关S,电烙铁处于预热状态;闭合S,电烙铁很快达到焊接温度.已知灯泡的灯丝在预热状态下电阻为790Ω,经测量,预热时通过电烙铁的电流为0.11A,设电烙铁的电阻不变,电源电压恒为220V,求:查看答案和解析>>
科目:初中物理 来源: 题型:
 电烙铁使用前需要一定的预热时间,因而若暂时不用也要接在电源上,这样既费电又会造成烙铁头氧化而不易沾锡.所以,有时采用如图8所示电路,在暂不需要焊接时,断开S,使电烙铁处于预热状态;当需焊接时,闭合S,就能很快达到焊接温度.现用“220V25W”的电烙铁,若灯炮在预热状态时的电阻为800欧,则预热状态下电烙铁消耗的功率为多少瓦?整个电路消耗的功率是电烙铁正常工作时的百分之几?
电烙铁使用前需要一定的预热时间,因而若暂时不用也要接在电源上,这样既费电又会造成烙铁头氧化而不易沾锡.所以,有时采用如图8所示电路,在暂不需要焊接时,断开S,使电烙铁处于预热状态;当需焊接时,闭合S,就能很快达到焊接温度.现用“220V25W”的电烙铁,若灯炮在预热状态时的电阻为800欧,则预热状态下电烙铁消耗的功率为多少瓦?整个电路消耗的功率是电烙铁正常工作时的百分之几?查看答案和解析>>
科目:初中物理 来源: 题型:
 电烙铁使用前需要一定的预热时间,即使不用也要将它接在电源上,但这样做既费电又会造成烙铁头氧化而不易沾锡,所以有时采用如图所示的电路,在暂不需要焊接时,断开开关S,使电烙铁处于保温状态;需要焊接时,闭合开关S就很快使电烙铁头达到焊接温度.若电烙铁的规格是“220V 40W”,要求电烙铁处于保温状态时的功率仅为其额定功率的
电烙铁使用前需要一定的预热时间,即使不用也要将它接在电源上,但这样做既费电又会造成烙铁头氧化而不易沾锡,所以有时采用如图所示的电路,在暂不需要焊接时,断开开关S,使电烙铁处于保温状态;需要焊接时,闭合开关S就很快使电烙铁头达到焊接温度.若电烙铁的规格是“220V 40W”,要求电烙铁处于保温状态时的功率仅为其额定功率的| 1 | 4 |
查看答案和解析>>
科目:初中物理 来源:2009-2010学年苏科版九年级(下)期中测试基础物理试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com