已知某型号的载重车在一段平直的高速公路上匀速行驶10.08km,所用时间是8min,消耗燃油3L(假设燃油完全燃烧),汽车发动机在这段时间内的功率为63kW.若燃油的密度是0.8×103kg/m3,热值为3.15×107J/kg,求:
(1)汽车行驶速度是多少?
(2)汽车行驶过程的牵引力是多大?
(3)汽车发动机的效率是多少?
已知:行驶的路程s=10.08km=10080m,所用时间是t=8min=480s,汽车发动机的功率为P=63kW=63000W,消耗燃油V=3L=3×10
-3m
3,燃油的密度是ρ=0.8×10
3kg/m
3,热值为q=3.15×10
7J/kg.
求:(1)汽车行驶速度v=?;(2)汽车行驶过程的牵引力F=?;(3)汽车发动机的效率η=?
解:(1)汽车行驶的速度:
v=

=
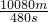
=21m/s;
(2)∵P=
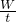
=
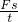
=Fv
∴汽车行驶过程的牵引力:
F=
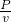
=
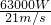
=3.0×10
3N;
(3)汽车行驶过程所做的功:
W=Pt=63000W×480s=3.024×10
7J,
∵ρ=

,
∴消耗的燃油的质量:
m=ρV=0.8×10
3kg/m
3×3×10
-3m
3=2.4kg,
燃油完全燃烧放出热量:
Q=qm=3.15×10
7J/kg×2.4kg=7.56×10
7J,
汽车发动机的效率是:
η=
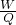
×100%=
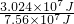
×100%=40%.
答:(1)汽车行驶速度是21m/s;
(2)汽车行驶过程的牵引力是3.0×10
3N;
(3)汽车发动机的效率是40%.
分析:(1)已知行驶的路程和所用的时间,根据公式v=

可求行驶速度.
(2)已知功率和速度,根据公式P=
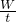
=
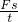
=Fv可求牵引力的大小.
(3)根据公式W=Pt可求汽车行驶过程所做的功,根据燃油的热值和燃烧燃油的质量求出燃油完全燃烧放出热量,二者之比就等于汽车发动机的效率.
点评:本题考查速度、牵引力和效率的计算,关键是公式及其变形的应用,难点是根据燃料的热值和体积以及密度求释放的热量.

 =
=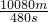 =21m/s;
=21m/s;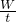 =
=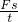 =Fv
=Fv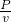 =
=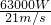 =3.0×103N;
=3.0×103N; ,
,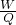 ×100%=
×100%=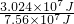 ×100%=40%.
×100%=40%. 可求行驶速度.
可求行驶速度.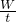 =
=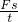 =Fv可求牵引力的大小.
=Fv可求牵引力的大小.
