一根绳子承受的最大拉力20N,用它去拉一个浸没在水中的2.7kg的铝块,如果铝块在水中匀速上升(不计水的阻力),则:
(1)绳子受到的拉力多大?
(2)铝块露出水面体积多大是绳子将被拉断?(ρ铝=2.7×103kg/m3,g=10N/kg)
解:(1)铝块的重:
G=mg=2.7kg×10N/kg=27N,
铝块的体积:
v=
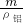
=
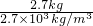
=0.001m
3,
浸没在水中的铝块的浮力:
F
浮=ρ
水gv
排=ρ
水gv=1.0×10
3kg/m
3×10N/kg×0.001m
3=10N,
∵F
拉+F
浮=G
∴F
拉=G-F
浮=27N-10N=17N;
(2)由题知,绳恰好断掉时水中的铝块受浮力:
F
浮′=G-F
大=27N-20N=7N,
铝块在水中的体积:
v
排′=
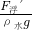
=
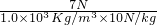
=0.0007m
3,
铝块露出水面的体积:
V
露=V-V
排′=0.001m
3-0.0007m
3=0.0003m
3答:(1)绳子受到的拉力为17N;
(2)铝块露出水面体积为0.0003m
3时绳子将被拉断.
分析:(1)知道铝块的质量,利用重力公式求铝块重;利用密度公式求铝块的体积,再利用阿基米德原理求铝块在水中受到的浮力.而浸没在水中的铝块受浮力、重力和绳的拉力,知道铝块匀速上升,铝块受到绳子的拉力加上浮力等于铝块重;据此求绳子受到的拉力.
(2)绳恰好断掉时绳的拉力为20N,此时水中的铝块受到得浮力等于铝块重减去绳子的拉力,根据阿基米德原理可计算铝块在水中的体积,铝块露出水面的体积V
露=V-V
排.
点评:本题为力学综合题,要求灵活运用密度公式、重力公式、阿基米德原理和力的合成,难度较大.

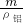 =
=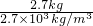 =0.001m3,
=0.001m3,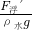 =
=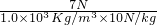 =0.0007m3,
=0.0007m3,

 阅读快车系列答案
阅读快车系列答案