
 如图所示,在一轻质的杠杆两端悬挂两个等质量的实心铁球和铝球,杠杆在水平位置平衡,将两球同时浸没在水中,则________端下沉,若要杠杆在水平位置再次平衡,应将支点向________端移动(选填“左”或“右”).铁球的体积为100cm3,当它浸没在水中静止时绳子对铁球的拉力为________N.(ρ铁=7.9×103kg/m3,取g=10N/kg)
如图所示,在一轻质的杠杆两端悬挂两个等质量的实心铁球和铝球,杠杆在水平位置平衡,将两球同时浸没在水中,则________端下沉,若要杠杆在水平位置再次平衡,应将支点向________端移动(选填“左”或“右”).铁球的体积为100cm3,当它浸没在水中静止时绳子对铁球的拉力为________N.(ρ铁=7.9×103kg/m3,取g=10N/kg)

科目:初中物理 来源: 题型:
 如图所示,有一轻质木板OA能绕O点转动,A端系细绳悬挂于墙上B点,并使A端上翘.在靠近A端处放着一小球,在小球沿木板滚下的过程中,细绳对木板的拉力将( )
如图所示,有一轻质木板OA能绕O点转动,A端系细绳悬挂于墙上B点,并使A端上翘.在靠近A端处放着一小球,在小球沿木板滚下的过程中,细绳对木板的拉力将( )查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,在一轻质的杠杆两端悬挂两个等质量的实心铁球和铝球,杠杆在水平位置平衡,将两球同时浸没在水中,则
如图所示,在一轻质的杠杆两端悬挂两个等质量的实心铁球和铝球,杠杆在水平位置平衡,将两球同时浸没在水中,则查看答案和解析>>
科目:初中物理 来源: 题型:
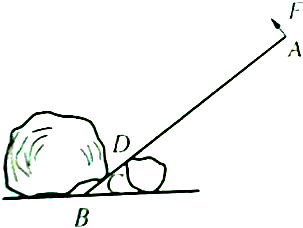 如图所示,有一轻质杠杆总长为1m,其中BC=CD=10cm,在力F的作用下,石头上的C点沿垂直于杠杆的方向移动了2cm,设力F的大小为100N,方向垂直于杠杆AB向上,则力F至少做了多少功?
如图所示,有一轻质杠杆总长为1m,其中BC=CD=10cm,在力F的作用下,石头上的C点沿垂直于杠杆的方向移动了2cm,设力F的大小为100N,方向垂直于杠杆AB向上,则力F至少做了多少功?查看答案和解析>>
科目:初中物理 来源:2011年湖南省长沙市中考物理模拟试卷(六)(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com