
 如图1所示,边长为0.1m的立方体A重30N,放在水平地面上,用水平拉力F拉着立方体A在水平地面上作匀速直线运动.已知运动过程中物体所受阻力为物重的0.01倍.(g取10N/kg)求:
如图1所示,边长为0.1m的立方体A重30N,放在水平地面上,用水平拉力F拉着立方体A在水平地面上作匀速直线运动.已知运动过程中物体所受阻力为物重的0.01倍.(g取10N/kg)求: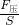 =
= =3000Pa;
=3000Pa;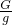 =
= =3kg,
=3kg, =
= =3×103kg/m3>1.0×103kg/m3,
=3×103kg/m3>1.0×103kg/m3,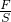 求出对地面的压强;
求出对地面的压强; 可求密度,然后与水的密度进行比较,判断出最终A静止时会处于什么状态,进一步求出浮力;
可求密度,然后与水的密度进行比较,判断出最终A静止时会处于什么状态,进一步求出浮力;

 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中物理 来源: 题型:
 (2013?镇江)如图1所示,边长为10cm的立方体木块A通过细线与圆柱形容器底部相连,容器中液面与A上表面齐平.从打开容器底部的抽液机匀速向外排液开始计时,细线中拉力F随时间t的变化图象如图2所示.木块密度ρ=0.5×103kg/m3,容器的底面积为200cm2,g=10N/kg.下列说法正确的是( )
(2013?镇江)如图1所示,边长为10cm的立方体木块A通过细线与圆柱形容器底部相连,容器中液面与A上表面齐平.从打开容器底部的抽液机匀速向外排液开始计时,细线中拉力F随时间t的变化图象如图2所示.木块密度ρ=0.5×103kg/m3,容器的底面积为200cm2,g=10N/kg.下列说法正确的是( )查看答案和解析>>
科目:初中物理 来源: 题型:
 如图1所示,边长为0.1m的立方体A重30N,放在水平地面上,用水平拉力F拉着立方体A在水平地面上作匀速直线运动.已知运动过程中物体所受阻力为物重的0.01倍.(g取10N/kg)求:
如图1所示,边长为0.1m的立方体A重30N,放在水平地面上,用水平拉力F拉着立方体A在水平地面上作匀速直线运动.已知运动过程中物体所受阻力为物重的0.01倍.(g取10N/kg)求:查看答案和解析>>
科目:初中物理 来源: 题型:
 (2011?咸宁)如图1所示将边长为10cm的密度均匀的正方体木块平放在圆柱形容器的底部,圆柱形容器的横截面积为300cm2,此时正方体木块对圆柱形容器的底部的压强是800N/m2.现缓慢地往容器中注水,当容器中的水面升至一定高度时,木块对容器底面的压力恰好为零,如图2所示.已知g=10N/kg,ρ水=1.0×103kg/m3.求:
(2011?咸宁)如图1所示将边长为10cm的密度均匀的正方体木块平放在圆柱形容器的底部,圆柱形容器的横截面积为300cm2,此时正方体木块对圆柱形容器的底部的压强是800N/m2.现缓慢地往容器中注水,当容器中的水面升至一定高度时,木块对容器底面的压力恰好为零,如图2所示.已知g=10N/kg,ρ水=1.0×103kg/m3.求:查看答案和解析>>
科目:初中物理 来源:2010年甘肃省张掖市高台县城关初中中考物理模拟试卷(二)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com