
 如图所示电路,小灯泡L标有“8V 3.2W”,滑动变阻器的最大阻值为40Ω,R1=18Ω.
如图所示电路,小灯泡L标有“8V 3.2W”,滑动变阻器的最大阻值为40Ω,R1=18Ω. 可得,灯泡L的电阻值:
可得,灯泡L的电阻值: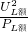 =
= =20Ω;
=20Ω;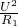 =
=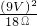 =4.5W;
=4.5W;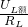 =
=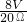 =0.4A,
=0.4A,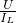 =
=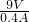 =22.5Ω,
=22.5Ω, =
= ,即
,即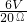 =
=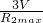 ,
, 求出灯泡L的电阻值;
求出灯泡L的电阻值; 求出R1上消耗的电功率;
求出R1上消耗的电功率;

科目:初中物理 来源: 题型:
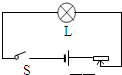 如图所示电路,小灯泡标有“6V 6W”字样,滑动变阻器标有“12Ω 2A”.闭合开关,滑动变阻器的滑片滑到最左端时,小灯泡正常发光.(设灯丝的电阻不变)滑动变阻器的滑片移动过程中以下说法正确的是( )
如图所示电路,小灯泡标有“6V 6W”字样,滑动变阻器标有“12Ω 2A”.闭合开关,滑动变阻器的滑片滑到最左端时,小灯泡正常发光.(设灯丝的电阻不变)滑动变阻器的滑片移动过程中以下说法正确的是( )| A、灯泡的实际功率最小值是2W | B、电源电压为12V | C、小灯泡两端的电压变化范围是2V~6V | D、灯丝电阻为8Ω |
查看答案和解析>>
科目:初中物理 来源: 题型:
 (2007?岳阳)小红同学用如图所示电路测小灯泡的电阻,记录数据如下表
(2007?岳阳)小红同学用如图所示电路测小灯泡的电阻,记录数据如下表
| 实验次数 | 1 | 2 | 3 |
| 电压U/V | 2.0 | 4.0 | 6.0 |
| 电流I/A | 0.15 | 0.20 | 0.25 |
| 电阻R/Ω | 13.3 | 20.0 | 24.0 |
| 灯泡发光情况 | 较暗 | 正常 | 较亮 |
| U |
| I |
| U |
| I |
查看答案和解析>>
科目:初中物理 来源: 题型:
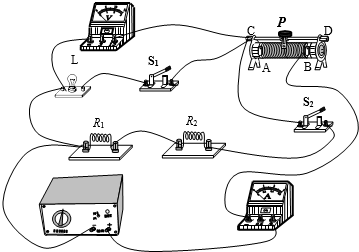
 (2013?道外区二模)某中学实践小组同学按如图所示电路探究小灯泡的工作情况.其中电源电压保持不变,灯L上标有“18V 18W”的字样,电压表所选量程为0~15V,电流表所选量程为0~3A.情况一:开关S闭合,滑动变阻器的滑片P移到a端时,灯L正常发光,电流表示数为2.5A;情况二:开关S断开,滑动变阻器的滑片P移到距a端四分之三ab长度时,电压表指针满偏.请回答以下问题:
(2013?道外区二模)某中学实践小组同学按如图所示电路探究小灯泡的工作情况.其中电源电压保持不变,灯L上标有“18V 18W”的字样,电压表所选量程为0~15V,电流表所选量程为0~3A.情况一:开关S闭合,滑动变阻器的滑片P移到a端时,灯L正常发光,电流表示数为2.5A;情况二:开关S断开,滑动变阻器的滑片P移到距a端四分之三ab长度时,电压表指针满偏.请回答以下问题:查看答案和解析>>
科目:初中物理 来源: 题型:
 某同学在用如图所示电路测小灯泡电阻的实验中,发现闭合开关以后,灯泡不亮,电流表没有示数,怎么移动滑动变阻器滑片位置,电压表的示数都不变,且均为电源电压.可能出现的问题是( )
某同学在用如图所示电路测小灯泡电阻的实验中,发现闭合开关以后,灯泡不亮,电流表没有示数,怎么移动滑动变阻器滑片位置,电压表的示数都不变,且均为电源电压.可能出现的问题是( )查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com