
 如图所示,底面积为2×10-2m2的圆柱形容器中装水.现将体积为10-3m3的正方体木块放入水中,木块静止时有
如图所示,底面积为2×10-2m2的圆柱形容器中装水.现将体积为10-3m3的正方体木块放入水中,木块静止时有 的体积露出水面.求:
的体积露出水面.求: V木 h=16cm=0.16m ρ水=1.0×103kg/m3
V木 h=16cm=0.16m ρ水=1.0×103kg/m3 )V木=
)V木= ×10-3m3=0.6×10-3m3
×10-3m3=0.6×10-3m3 F压=
F压= ×3.92N=1.96N,
×3.92N=1.96N, =
=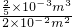 =0.02m,
=0.02m,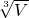 =
= =0.1m,
=0.1m,

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中物理 来源: 题型:
 (2003?长沙)如图所示,底面积为0.1㎡的物体A重300N,受到一水平拉力F作用,物体A在水平地面作匀速直线运动.已知运动过程中物体所受阻力为物重的0.1倍.求:
(2003?长沙)如图所示,底面积为0.1㎡的物体A重300N,受到一水平拉力F作用,物体A在水平地面作匀速直线运动.已知运动过程中物体所受阻力为物重的0.1倍.求:查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,底面积为2×10-2m2的圆柱形容器中装水.现将体积为10-3m3的正方体木块放入水中,木块静止时有
如图所示,底面积为2×10-2m2的圆柱形容器中装水.现将体积为10-3m3的正方体木块放入水中,木块静止时有| 2 | 5 |
查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示:底面积为80cm2的容器中盛有30cm深的水,现将一质量为540g的实心铝球投入水中,(ρ铝=2.7g/cm3 g取10N/Kg)问:
如图所示:底面积为80cm2的容器中盛有30cm深的水,现将一质量为540g的实心铝球投入水中,(ρ铝=2.7g/cm3 g取10N/Kg)问:查看答案和解析>>
科目:初中物理 来源:2011-2012学年湖北省黄冈市麻城市龟山中心学校九年级(上)月考物理试卷(解析版) 题型:解答题
 的体积露出水面.求:
的体积露出水面.求:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com