
 如图所示,B、C两点相距60米,C、A两点相距80米,AC与BC相互垂直.甲以2米/秒的速度由B点向C点运动,乙以4米/秒的速度同时由C点向A点运动.经过________秒,甲、乙之间的距离最近;经过________秒,甲、乙所处位置与C点构成的三角形和三角形ABC可能相似.
如图所示,B、C两点相距60米,C、A两点相距80米,AC与BC相互垂直.甲以2米/秒的速度由B点向C点运动,乙以4米/秒的速度同时由C点向A点运动.经过________秒,甲、乙之间的距离最近;经过________秒,甲、乙所处位置与C点构成的三角形和三角形ABC可能相似.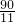 或12
或12 时二次函数有最小值.如图1.
时二次函数有最小值.如图1.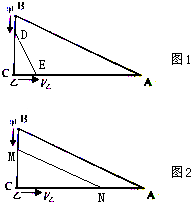
 =-
=-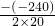 =6s时,y最小,即甲乙距离最短.
=6s时,y最小,即甲乙距离最短.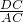 =
= ,
,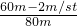 =
=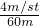 .
.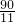 s.
s.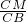 =
=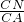 ,
,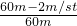 =
= ,
,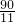 或12.
或12.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中物理 来源: 题型:
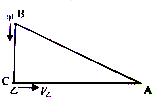 如图所示,B、C两点相距60米,C、A两点相距80米,AC与BC相互垂直.甲以2米/秒的速度由B点向C点运动,乙以4米/秒的速度同时由C点向A点运动.经过
如图所示,B、C两点相距60米,C、A两点相距80米,AC与BC相互垂直.甲以2米/秒的速度由B点向C点运动,乙以4米/秒的速度同时由C点向A点运动.经过| 90 |
| 11 |
| 90 |
| 11 |
查看答案和解析>>
科目:初中物理 来源: 题型:阅读理解
 (2010?青浦区二模)在做“探究导体中电流与电压的关系”实验时,某小组同学利用A、B、C三个不同的导体作为研究对象分别接在如图所示的M、N两点间进行实验.表一、表二和表三为该小组同学的实验记录表.
(2010?青浦区二模)在做“探究导体中电流与电压的关系”实验时,某小组同学利用A、B、C三个不同的导体作为研究对象分别接在如图所示的M、N两点间进行实验.表一、表二和表三为该小组同学的实验记录表.
| 表一 | 表二 | 表三 | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
查看答案和解析>>
科目:初中物理 来源: 题型:
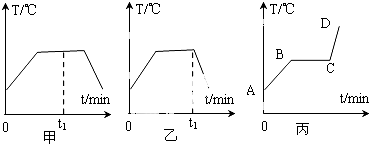
查看答案和解析>>
科目:初中物理 来源:2009年上海市第二十三届初中物理竞赛初赛试卷(大同中学杯)(解析版) 题型:填空题
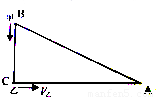
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com