【答案】
分析:(1)为保护电路,连接电路时开关应断开;
(2)根据灯泡额定电压确定电压表量程,根据灯泡正常发光时的电流确定电流表量程,
滑动变阻器、灯泡、电流表、开关串联接入电路,电压表并联在灯泡两端;
连线时注意滑动变阻器的接法,注意电压表与电流表正负接线柱不要接反;
(3)为保护电路,闭合开关前,滑动变阻器接入电路的阻值应为滑动变阻器的最大阻值;
(4)灯泡不亮,可能是灯泡断路或灯泡短路;电流表无示数,说明电路存在断路;电压表示数等于电源电压,说明电压表与电源两极相连,电压表并联电路之外不存在断路;
(5)根据图乙读出电压表示数,根据该示数与灯泡额定电压间的关系,判断滑片的移动方向,知道电压表示数等于灯泡额定电压为止.
(6)由I-U图象找出灯泡额定电压对应的电流,然后由功率公式P=UI和R=
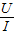
求出灯泡的额定功率和电阻;灯丝的电阻随温度的变化而变化.
(7)用15Ω的电阻替换10Ω的电阻,闭合开关后,由于电路总电阻变大,电路电流变小,滑动变阻器两端电压变大,由于电源电压变大,由串联电路的特点知,电阻两端电压变大,要保持电阻两端电压不变,应移动滑动变阻器滑片,使滑动变阻器接入电路的阻值变大,灯泡两端的电压减小,以保证电阻两端的电压保持不变.
根据表中电阻与电流的积不变得出结论.
解答:解:(1)在连接电路时,开关应处于断开状态;
(2)灯泡额定电压是2.5V,则电压表选3V量程;灯泡正常发光时的电流约为I=

=

=0.25A,则电流表应选0~0.6A量程;
滑动变阻器、灯泡、电流表、开关串联接入电路,电压表并联在灯泡两端,电路图如图所示;
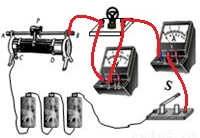
(3)由实物电路图知,当滑动变阻器滑片在B端时,滑动变阻器接入电路的阻值最大,因此闭合开关前,滑动变阻器的滑片P应位于B端;
(4)闭合开关,发现灯泡不亮,电流表无示数,电压表示数等于电源电压,其故障可能是:灯泡断路.
(5)已知电压表量程是0~3V,分度值是0.1V,则电压表示数是2.2V,小于灯泡额定电压,要使灯泡正常发光应向A移动滑动变阻器滑片P,使滑动变阻器接入电路的阻值变小,灯泡两端电压增大,直到电压表示数等于灯泡额定电压2.5V为止.
(6)由图象I-U知,灯泡的额定电压U=2.5V对应的电流I=0.2A,灯泡额定功率P=UI=2.5V×0.2A=0.5W;此时灯泡的电阻R=
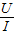
=

=12.5Ω;因为灯丝的电阻与温度有关,因此电压和电流的图象为曲线.
(7)由表中实验数据知,电阻两端的电压为5Ω×0.6A=3V保持不变;为保证电阻两端的电压保持不变,用15Ω的电阻替换10Ω的电阻,闭合开关后,应将滑动变阻器的滑片P向B端移动,使电压表的示数为3V,完成第三次实验;
根据表中数据可知,电流与电阻的乘积不变,故可得出的结论为:电压一定时,电阻与电流成反比.
故答案为:(1)断开;(3)B;(4)灯泡断路;(5)A;(6)0.5;12.5;灯丝电阻受温度影响;(7)B;3;电压一定时,电阻与电流成反比.
点评:本题考查了测量小灯泡电功率的实验,涉及到电路图的连接、电路故障的判断、电压表的读数、串联电路的分压作用及额定功率的计算,同时还考查了学生对图象的分析和处理能力,本实验需要注意灯丝的电阻随温度的变化而变化以及控制变量法的应用.


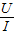 求出灯泡的额定功率和电阻;灯丝的电阻随温度的变化而变化.
求出灯泡的额定功率和电阻;灯丝的电阻随温度的变化而变化. =
= =0.25A,则电流表应选0~0.6A量程;
=0.25A,则电流表应选0~0.6A量程;
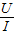 =
= =12.5Ω;因为灯丝的电阻与温度有关,因此电压和电流的图象为曲线.
=12.5Ω;因为灯丝的电阻与温度有关,因此电压和电流的图象为曲线.

 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案



 小明在做“测定小灯泡额定功率”的实验时,电源电压为6.0V,小灯泡的额定电压为3.8V,阻值约为12Ω.如图甲所示是小勇同学连接的实物电路.
小明在做“测定小灯泡额定功率”的实验时,电源电压为6.0V,小灯泡的额定电压为3.8V,阻值约为12Ω.如图甲所示是小勇同学连接的实物电路.