
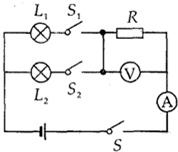
 额定电压为3V的灯泡L1和额定电压为6V的灯泡L2组成如图所示的电路,R为定值电阻,已知电源电压保持不变,若闭合开关S、S1,断开S2,L1实际功率为其额定功率的1/4,电压表的示数为4.5V;若闭合开关S、S2,断开S1,电压表的示数为3V;若铜时闭合开关S、S1、S2,电流表的示数为0.4A.求:
额定电压为3V的灯泡L1和额定电压为6V的灯泡L2组成如图所示的电路,R为定值电阻,已知电源电压保持不变,若闭合开关S、S1,断开S2,L1实际功率为其额定功率的1/4,电压表的示数为4.5V;若闭合开关S、S2,断开S1,电压表的示数为3V;若铜时闭合开关S、S1、S2,电流表的示数为0.4A.求: ,且灯泡L1实际功率为其额定功率的
,且灯泡L1实际功率为其额定功率的 和额定电压为3V,
和额定电压为3V,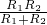 +R=
+R=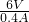 --------③
--------③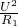 =
=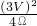 =2.25W;
=2.25W;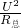 =
=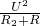 =
=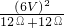 =1.5W.
=1.5W. 可知L1实际功率为其额定功率的
可知L1实际功率为其额定功率的 时L1电压,再根据串联电路的电压特点求出电源的电压,再根据串联电路电阻的分压特点可知它们电阻之间的关系;
时L1电压,再根据串联电路的电压特点求出电源的电压,再根据串联电路电阻的分压特点可知它们电阻之间的关系; 求出L1的额定功率;
求出L1的额定功率; 可知当电路中的电阻最大时电路中的电功率最小,根据电阻的串联特点和并联特点可知当闭合开关S、S2,断开S1时,电路中功率最小,利用P=
可知当电路中的电阻最大时电路中的电功率最小,根据电阻的串联特点和并联特点可知当闭合开关S、S2,断开S1时,电路中功率最小,利用P= 求出电路最小功率.
求出电路最小功率. 时L1电压,难点是根据已知条件建立方程求出灯泡和R的阻值.
时L1电压,难点是根据已知条件建立方程求出灯泡和R的阻值. 

科目:初中物理 来源: 题型:
 (2009?江苏二模)额定电压为3V的灯泡L1和额定电压为6V的灯泡L2组成如图所示的电路,R为定值电阻,已知电源电压保持不变,若闭合开关S、S1,断开S2,L1实际功率为其额定功率的1/4,电压表的示数为4.5V;若闭合开关S、S2,断开S1,电压表的示数为3V;若铜时闭合开关S、S1、S2,电流表的示数为0.4A.求:
(2009?江苏二模)额定电压为3V的灯泡L1和额定电压为6V的灯泡L2组成如图所示的电路,R为定值电阻,已知电源电压保持不变,若闭合开关S、S1,断开S2,L1实际功率为其额定功率的1/4,电压表的示数为4.5V;若闭合开关S、S2,断开S1,电压表的示数为3V;若铜时闭合开关S、S1、S2,电流表的示数为0.4A.求:查看答案和解析>>
科目:初中物理 来源:2010-2011学年江苏省泰州市海陵区初三中考物理适应性训练 题型:填空题
额定电压为3V的灯泡,正常发光时通过灯丝的电流是0.5A,则该灯泡的额定功率是 W
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com