轮船朝码头开去,速度为10m/s,船员看到码头高大建筑物时鸣笛,3s后船员听到回声.问:
(1)鸣笛时轮船码头多远?
(2)听到回声时,轮船离码头多远?
【答案】
分析:(1)鸣笛后,声音传到建筑物返回轮船时,轮船以10m/s的速度已经前行了3s,在这段时间内,声音和轮船两者行驶的路程之和是鸣笛时轮船与建筑物距离的2倍,根据速度公式求出两者的路程即可解题.
(2)听到回声时,声音和轮船两者行驶的路程之差是听到回声时轮船与建筑物距离的2倍.
解答:已知:轮船速度v
船=10m/s,声音的传播速度v
声=340m/s,听到回声的时间t=3s
求:(1)鸣笛时轮船离码头的距离s=?;(2)听到回声时轮船离码头距离s′=?
解:(1)∵v=

,
∴轮船行驶的距离:
s
船=v
船t=10m/s×3s=30m,
声音传播的距离:
s
声=v
声t=340m/s×3s=1020m,
所以,鸣笛时轮船离码头的距离:
s=
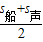
=
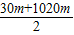
=525m;
(2)听到回声时轮船离码头距离:
s′=
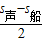
=
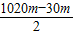
=495m.
答:(1)鸣笛时轮船离码头的距离为525m;
(2)听到回声时,轮船离码495m.
点评:此题主要考查的是学生对速度计算公式的理解和掌握,解题的关键是分析清楚声音和汽车两者行驶的路程之和是鸣笛时汽车与山脚距离的2倍;听到回声时,声音和轮船两者行驶的路程之差是听到回声时轮船与建筑物距离的2倍.

 ,
,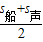 =
=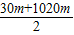 =525m;
=525m;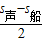 =
=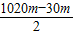 =495m.
=495m.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案