
 如图所示,横截面为四分之一圆(半径为R)的柱体放在水平地面上,一根匀质木棒OA长为3R,重为G.木棒的O端与地面上的铰链连接,木棒搁在柱体上,各处摩擦均不计.现用一水平推力F作用在柱体竖直面上,使柱体沿着水平地面向左缓慢移动.问:
如图所示,横截面为四分之一圆(半径为R)的柱体放在水平地面上,一根匀质木棒OA长为3R,重为G.木棒的O端与地面上的铰链连接,木棒搁在柱体上,各处摩擦均不计.现用一水平推力F作用在柱体竖直面上,使柱体沿着水平地面向左缓慢移动.问: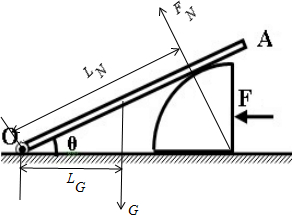 解:(1)如图示,重力的力臂LG=
解:(1)如图示,重力的力臂LG=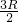 cosθ=
cosθ=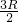 cos30°=
cos30°=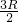 ×
× =
=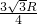 ,柱体与木棒的弹力力臂LN=
,柱体与木棒的弹力力臂LN=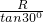 =
= R,
R,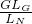 =
=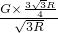 =
=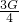
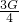 ×
× =
= .
. .
.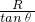 ,GLG=FNLN,FN=
,GLG=FNLN,FN=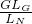 =
=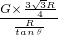 =
=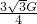 tanθ,在柱体缓慢向左移动的过程中,θ不断变大,从而tanθ不断变大,FN不断变大.
tanθ,在柱体缓慢向左移动的过程中,θ不断变大,从而tanθ不断变大,FN不断变大. G.(2)此时水平推力为
G.(2)此时水平推力为 G.(3)在柱体向左缓慢移动过程中,柱体对木棒的弹力及水平推力F都不断变大.
G.(3)在柱体向左缓慢移动过程中,柱体对木棒的弹力及水平推力F都不断变大.

科目:初中物理 来源: 题型:
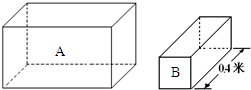 (2011?嘉定区一模)如图所示,横截面为正方形的实心均匀长方体A、B放置在水平地面上,它们的高度分别为0.2米和0.1米,B的另一条边长为0.4米,A的密度为2×103千克/米3,B质量为1千克.
(2011?嘉定区一模)如图所示,横截面为正方形的实心均匀长方体A、B放置在水平地面上,它们的高度分别为0.2米和0.1米,B的另一条边长为0.4米,A的密度为2×103千克/米3,B质量为1千克.查看答案和解析>>
科目:初中物理 来源: 题型:
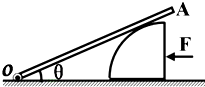 如图所示,横截面为四分之一圆(半径为R)的柱体放在水平地面上,一根匀质木棒OA长为3R,重为G.木棒的O端与地面上的铰链连接,木棒搁在柱体上,各处摩擦均不计.现用一水平推力F作用在柱体竖直面上,使柱体沿着水平地面向左缓慢移动.当木棒与地面的夹角θ=30°时,柱体对木棒的支持力为
如图所示,横截面为四分之一圆(半径为R)的柱体放在水平地面上,一根匀质木棒OA长为3R,重为G.木棒的O端与地面上的铰链连接,木棒搁在柱体上,各处摩擦均不计.现用一水平推力F作用在柱体竖直面上,使柱体沿着水平地面向左缓慢移动.当木棒与地面的夹角θ=30°时,柱体对木棒的支持力为查看答案和解析>>
科目:初中物理 来源: 题型:
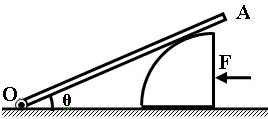 如图所示,横截面为四分之一圆(半径为R)的柱体放在水平地面上,一根匀质木棒OA长为3R,重为G.木棒的O端与地面上的铰链连接,木棒搁在柱体上,各处摩擦均不计.现用一水平推力F作用在柱体竖直面上,使柱体沿着水平地面向左缓慢移动.问:
如图所示,横截面为四分之一圆(半径为R)的柱体放在水平地面上,一根匀质木棒OA长为3R,重为G.木棒的O端与地面上的铰链连接,木棒搁在柱体上,各处摩擦均不计.现用一水平推力F作用在柱体竖直面上,使柱体沿着水平地面向左缓慢移动.问:查看答案和解析>>
科目:初中物理 来源: 题型:填空题
 如图所示,横截面为四分之一圆(半径为R)的柱体放在水平地面上,一根匀质木棒OA长为3R,重为G.木棒的O端与地面上的铰链连接,木棒搁在柱体上,各处摩擦均不计.现用一水平推力F作用在柱体竖直面上,使柱体沿着水平地面向左缓慢移动.当木棒与地面的夹角θ=30°时,柱体对木棒的支持力为________.
如图所示,横截面为四分之一圆(半径为R)的柱体放在水平地面上,一根匀质木棒OA长为3R,重为G.木棒的O端与地面上的铰链连接,木棒搁在柱体上,各处摩擦均不计.现用一水平推力F作用在柱体竖直面上,使柱体沿着水平地面向左缓慢移动.当木棒与地面的夹角θ=30°时,柱体对木棒的支持力为________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com