
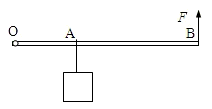
 如图所示OB为粗细均匀的均质杠杆,O为支点,在离O点距离为a的A处挂一个质量为M的物体,杠杆每单位长度的质量为m,当杠杆为多长时,可以在B点用最小的作用力F维持杠杆平衡?
如图所示OB为粗细均匀的均质杠杆,O为支点,在离O点距离为a的A处挂一个质量为M的物体,杠杆每单位长度的质量为m,当杠杆为多长时,可以在B点用最小的作用力F维持杠杆平衡?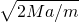
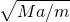
 OB),明确了动力、动力臂、阻力和阻力臂之后,我们就可以根据杠杆平衡条件列出一个方程,然后根据数学方面的知识求解方程.
OB),明确了动力、动力臂、阻力和阻力臂之后,我们就可以根据杠杆平衡条件列出一个方程,然后根据数学方面的知识求解方程. OB,重物的重力G物=Mg
OB,重物的重力G物=Mg OB,
OB, OB,
OB, mg?(OB)2,
mg?(OB)2, mg?(OB)2-F?OB+Mga=0,
mg?(OB)2-F?OB+Mga=0, mg×Mga=0,
mg×Mga=0, ?g,
?g, ?g代入方程
?g代入方程 mg?(OB)2-F?OB+Mga=0,
mg?(OB)2-F?OB+Mga=0, .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中物理 来源: 题型:
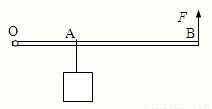
 如图所示OB为粗细均匀的均质杠杆,O为支点,在离O点距离为a的A处挂一个质量为M的物体,杠杆每单位长度的质量为m,当杠杆为多长时,可以在B点用最小的作用力F维持杠杆平衡?( )
如图所示OB为粗细均匀的均质杠杆,O为支点,在离O点距离为a的A处挂一个质量为M的物体,杠杆每单位长度的质量为m,当杠杆为多长时,可以在B点用最小的作用力F维持杠杆平衡?( )查看答案和解析>>
科目:初中物理 来源:2010年浙江省第五届初中自然科学竞赛复赛试卷(解析版) 题型:选择题
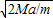
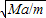
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com