Question

运用知识解决问题：
（1）画出图中力F的力臂．
（2）将石块放入盛满水的烧杯中时，溢出了10cm³的水，石块受到的浮力是______N．（g=10N/kg）
（3）甲、乙两车都从A地出发，沿同一条路运行，甲比乙先出发半小时，甲车的速度为10m/s，乙车的速度为54km/h，问甲乙两车相遇时，离甲的出发点多远？

Answer 1

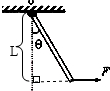
解：（1）反向延长力的作用线F，则支点O到力的作用线的垂线段，即为F的力臂，如图所示：

（2）已知V=10cm³=10×10^-6m³，m=ρV=1.0×10³kg/m³×10×10^-6m³=0.01N，
则F_浮=G_排=mg=0.01N×10N/kg=0.1N．
故答案为：0.1N．
（3）S_甲=v_甲t_甲=10m/s×t_甲=36km/h×t_甲，
S_乙=v_乙t_乙=54km/h×t_乙，
又∵相遇即追上，则S_甲=S_乙，
∴36km/h×t_甲=54km/h×t_乙，
∴2t_甲=3t_乙，
又∵t_甲-0.5h=t_乙，
∴t_乙=1h，
则t_甲=1．h
∴S_甲=36km/h×t_甲=36km/h×1.5h=54km．
答：离甲的出发点54km．
分析：（1）已知支点和力F的方向，根据力臂的画法，过支点作力的作用线的垂线段，即为F的力臂．
（2）已知溢出的水的体积可求出其质量，利用G=mg可求出其重力，根据阿基米德原理，浸入液体中的物体所受浮力大小等于它排开的液体的重力．
（3）首先明确甲乙两车相遇时，即相遇即追上，则根据相遇时二人所走的路程相同列出等式S_甲=S_乙，再根据甲比乙先出发半小时，列出关系式t_甲-0.5=t_乙，然后问题可解．
点评：此题考查力臂的画法，画出相应力的力臂，并且要求作图规范．还考查学生对阿基米德原理以及速度公式的理解和掌握，计算时要注意单位的统一．