
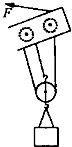
 如图所示,是某建筑工地所用的起重机的吊臂上的滑轮组,由电动机向滑轮组提供动力.若用该滑轮组匀速提升质量为500kg的物体,在重物上升0.8m的过程中,拉力F的2000N,求:
如图所示,是某建筑工地所用的起重机的吊臂上的滑轮组,由电动机向滑轮组提供动力.若用该滑轮组匀速提升质量为500kg的物体,在重物上升0.8m的过程中,拉力F的2000N,求: ×100%=
×100%= ×100%=≈83.3%;
×100%=≈83.3%; =
=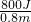 =1000N;
=1000N; (G物+G动)=
(G物+G动)= ×(8000N+1000N)=3000N.
×(8000N+1000N)=3000N. 求出滑轮组的机械效率;
求出滑轮组的机械效率; (G物+G动)求出第二次的拉力.
(G物+G动)求出第二次的拉力.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中物理 来源: 题型:
 我校高中部建筑工地运来一个边长为a的正方体重物箱,某工人欲用一根粗细均匀的铁棒把重物箱撬起一个很小的角度(如图所示,图中的角度已被放大).已知:铁棒单位长度受到的重力为P;重物箱受到的重力为G(重物箱的密度均匀).工人将铁棒的一端插入箱底,在另一端施加一个向上的力撬动重物箱.如果插入的长度为箱宽的四分之一,并保持该长度不变,请你通过计算帮他分析,当选用的铁棒长度满足什么条件时,施加的力最小?这个最小的力是多少?
我校高中部建筑工地运来一个边长为a的正方体重物箱,某工人欲用一根粗细均匀的铁棒把重物箱撬起一个很小的角度(如图所示,图中的角度已被放大).已知:铁棒单位长度受到的重力为P;重物箱受到的重力为G(重物箱的密度均匀).工人将铁棒的一端插入箱底,在另一端施加一个向上的力撬动重物箱.如果插入的长度为箱宽的四分之一,并保持该长度不变,请你通过计算帮他分析,当选用的铁棒长度满足什么条件时,施加的力最小?这个最小的力是多少?查看答案和解析>>
科目:初中物理 来源: 题型:
 (2010?南通模拟)在某建筑工地上,工人用如图所示的滑轮组将重为1200N的建筑材料从地面上运到高10m的楼上,在这个过程中,工人做了
(2010?南通模拟)在某建筑工地上,工人用如图所示的滑轮组将重为1200N的建筑材料从地面上运到高10m的楼上,在这个过程中,工人做了查看答案和解析>>
科目:初中物理 来源: 题型:
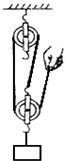 在某建筑工地上,工人用如图所示的滑轮组将重为1200N的建筑材料从地面运到高20m的楼上,手竖直向上的拉力是500N,拉力移动距离
在某建筑工地上,工人用如图所示的滑轮组将重为1200N的建筑材料从地面运到高20m的楼上,手竖直向上的拉力是500N,拉力移动距离查看答案和解析>>
科目:初中物理 来源: 题型:
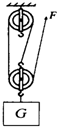 (2011?广东二模)在某建筑工地上,工人用如图所示的滑轮组将重为1200N的建筑材料从地面运到高20m的楼上,手竖直向上的拉力是500N,在这个过程中,工人做了
(2011?广东二模)在某建筑工地上,工人用如图所示的滑轮组将重为1200N的建筑材料从地面运到高20m的楼上,手竖直向上的拉力是500N,在这个过程中,工人做了查看答案和解析>>
科目:初中物理 来源: 题型:
 在某建筑工地上,工人师傅用如图所示的滑轮组将重为600N的建筑材料从地面匀速运到楼上,如果不计摩擦力、动滑轮重力和绳子重力,则手对绳端的拉力是( )
在某建筑工地上,工人师傅用如图所示的滑轮组将重为600N的建筑材料从地面匀速运到楼上,如果不计摩擦力、动滑轮重力和绳子重力,则手对绳端的拉力是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com