
 实验室中“测量滑轮组的机械效率”的实验装置如图所示,每个滑轮组下面挂4个钩码,每个钩码重0.5N,每个滑轮所受的重力相等且小于0.2N.
实验室中“测量滑轮组的机械效率”的实验装置如图所示,每个滑轮组下面挂4个钩码,每个钩码重0.5N,每个滑轮所受的重力相等且小于0.2N. ×100%=
×100%= ×100%≈83.3%;
×100%≈83.3%; ×100%=
×100%= ×100%=
×100%=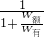 ×100%可知,η甲>η乙.
×100%可知,η甲>η乙. ×100%求出滑轮组的机械效率;
×100%求出滑轮组的机械效率;

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中物理 来源: 题型:
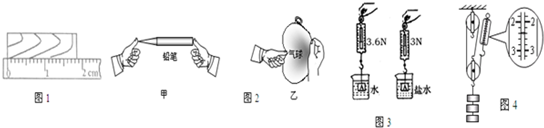
 (2008?贵港)实验室中“测量滑轮组的机械效率”的实验装置如图所示,每个滑轮组下面挂4个钩码,每个钩码重0.5N,每个滑轮所受的重力相等且小于0.2N.
(2008?贵港)实验室中“测量滑轮组的机械效率”的实验装置如图所示,每个滑轮组下面挂4个钩码,每个钩码重0.5N,每个滑轮所受的重力相等且小于0.2N.查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源:贵港 题型:问答题
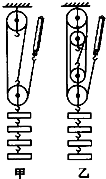
查看答案和解析>>
科目:初中物理 来源:2008年广西贵港市中考物理试卷(解析版) 题型:解答题
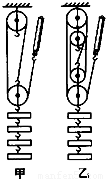
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com