
 =
=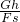 =
=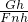 =
= ,
, =
=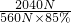 =5;
=5; 得:
得: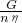 =
=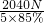 =480N.
=480N. ,
,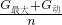 得:
得: =
=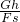 =
=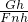 =
= 求出n的大小,即承担物重的绳子股数,然后根据“奇动偶定”确定滑轮组的绕线方法,进一步得出需要滑轮的个数.
求出n的大小,即承担物重的绳子股数,然后根据“奇动偶定”确定滑轮组的绕线方法,进一步得出需要滑轮的个数. 得到的F拉=
得到的F拉=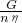 计算出人实际拉力的大小.
计算出人实际拉力的大小. 即可求出重物的重力.
即可求出重物的重力.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中物理 来源: 题型:
 (2010?平谷区二模)如图所示,是利用器械提升重物的示意图.当某人自由站在水平地面上时,他对地面的压强P0=2×104Pa;当滑轮下未挂重物时,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P1=2.375×104Pa;当滑轮下加挂重物G后,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P2=5.75×104Pa.假设这个人用的力和绳端B用的力始终沿竖直方向,加挂重物前后他对杠杆A端施加的举力分别为F1、F2,已知F2=1500N.(杠杆、绳重和机械间摩擦忽略不计,g取10N/kg)
(2010?平谷区二模)如图所示,是利用器械提升重物的示意图.当某人自由站在水平地面上时,他对地面的压强P0=2×104Pa;当滑轮下未挂重物时,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P1=2.375×104Pa;当滑轮下加挂重物G后,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P2=5.75×104Pa.假设这个人用的力和绳端B用的力始终沿竖直方向,加挂重物前后他对杠杆A端施加的举力分别为F1、F2,已知F2=1500N.(杠杆、绳重和机械间摩擦忽略不计,g取10N/kg)查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
 (2012?大兴区一模)如图所示,是利用器械提升重物的示意图.当某人自由站在水平地面上时,他对地面的压强P0=2×104Pa;当滑轮下未挂重物时,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P1=2.375×104Pa;当滑轮下加挂重物G后,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P2=5.75×104Pa.假设这个人用的力和绳端B用的力始终沿竖直方向.(杠杆、绳重和机械间摩擦忽略不计)则当重物G被匀速提升过程中,滑轮组的机械效率为
(2012?大兴区一模)如图所示,是利用器械提升重物的示意图.当某人自由站在水平地面上时,他对地面的压强P0=2×104Pa;当滑轮下未挂重物时,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P1=2.375×104Pa;当滑轮下加挂重物G后,他用力匀速举起杠杆的A端,使杠杆在水平位置平衡时,他对地面的压强P2=5.75×104Pa.假设这个人用的力和绳端B用的力始终沿竖直方向.(杠杆、绳重和机械间摩擦忽略不计)则当重物G被匀速提升过程中,滑轮组的机械效率为查看答案和解析>>
科目:初中物理 来源:2012年江苏省淮安市涟水县徐集中学中考物理模拟试卷(四)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com