用密度为2.7×103kg/m3的铝制成甲、乙、丙三个大小不同的正方体.要求它们的边长分别是0.1m、0.2m和0.3m,制成后让质量检查员称出它们的质量,分别是3kg、21.6kg和54kg,质量检查员指出,有两个不合格,其中一个掺入了杂质为次品,另一个混入了空气泡为废品,则这三个正方体( )
A.甲为废品,乙为合格品,丙为次品
B.甲为合格品,乙为废品,丙为次品
C.甲为次品,乙为合格品,丙为废品
D.甲为废品,乙为次品,丙为合格品
【答案】
分析:先分别算出甲、乙、丙三个正方体的体积,然后用它们的质量除以它们的体积算出它们各自的密度,最后将算得的密度与铝的密度进行比较:相等的为合格品,比铝的密度小的是废品(混入空气,则在相同体积情况下,质量会变小,所以密度会变小),剩下的那一个就是次品.
解答:解:甲的体积:V
甲=0.1m×0.1m×0.1m=0.001m
3,则甲的密度:ρ
甲=
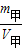
=

=3×10
3kg/m
3;
乙的体积:V
乙=0.2m×0.2m×0.2m=0.008m
3,则乙的密度:ρ
乙=
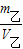
=
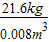
=2.7×10
3kg/m
3;
丙的体积:V
丙=0.3m×0.3m×0.3m=0.027m
3,则丙的密度:ρ
丙=
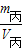
=

=2×10
3kg/m
3.
因为ρ
乙=ρ
铝,所以乙是合格品;因为ρ
丙<ρ
铝,所以丙是废品;因为ρ
甲>ρ
铝,所以甲是次品.
故选 C.
点评:因为密度是物质的一种特性,所以我们可以利用密度来鉴别物质.解答该题的思路就是分别算出三个正方体的密度,然后和铝的密度进行比较.

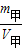 =
= =3×103kg/m3;
=3×103kg/m3;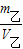 =
=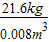 =2.7×103kg/m3;
=2.7×103kg/m3;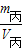 =
= =2×103kg/m3.
=2×103kg/m3.

 口算能手系列答案
口算能手系列答案