Question

同一容器中装有密度不同且不能混合的三种液体，甲、乙、丙三条有阀门的细管均与大气相通，如图所示．打开阀门后，管内液面高度正确的是

1. A.
   甲管内液面与容器内液面相平
2. B.
   甲、乙、丙三条管内液面相平
3. C.
   甲管液面最低，丙管液面最高
4. D.
   甲管液面最高，丙管液面最低

Answer 1

D
分析：根据连通器原理判断甲管内的液面和容器内液面相平．
由于打开阀门后，乙管和容器交界的液片AB₂和丙管和容器交界的液片AB₃都处于静止状态，受到的向左和向右的压力相同，压强相同．
把乙管分成两部分，其中的h_2B产生的压强和h'₂产生的压强相等，h_2A产生的压强和h₁产生的压强相等，由于密度的不同，判断液体深度的大小．
把丙管分成三部分，其中的h_3C产生的压强和h'₃产生的压强相等，h_3B产生的压强和h''₂产生的压强相等，h_3A产生的压强和h₁、h'₂产生的压强相等，由于密度的不同，判断液体深度的大小．
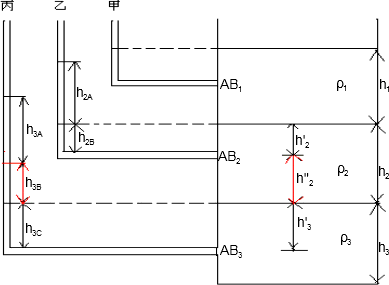
解答：解：由于三种液体不相混合，从图可知，ρ₁＜ρ₂＜ρ₃，
当打开甲、乙、丙三个阀门时，
甲管：甲管和容器上层形成一个连通器，甲管和容器的上层都装有ρ₁，静止时液面是相平的．
乙管：液体静止，乙管和容器交界的液片AB₂处于静止状态，受到的向左和向右的压力相同，向左和向右压强相同．
所以，ρ₂gh_2A+ρ₂gh_2B=ρ₁gh₁+ρ₂gh'₂，
因为h_2B与h'₂等高，所以ρ₂gh_2B=ρ₂gh'₂，
所以ρ₂gh_2A=ρ₁gh₁，
又因为ρ₂＞ρ₁，
所以，h_2A＜h₁，
所以，h_2A+h_2B＜h₁+h'₂，
所以乙管液面低于甲管液面．
丙管：液体静止，丙管和容器交界的液片AB₃处于静止状态，受到的向左和向右的压力相同，向左和向右压强相同．
所以，ρ₃gh_3A+ρ₃gh_3B+ρ₃gh_3C=ρ₁gh₁+ρ₂gh₂+ρ₃gh'₃，
因为h_3C与h'₃等高，--①
所以ρ₃gh_3C=ρ₃gh'₃，所以，ρ₃gh_3A+ρ₃gh_3B=ρ₁gh₁+ρ₂gh₂，
把液体ρ₂分成两段h'₂和h''₂，
ρ₃gh_3A+ρ₃gh_3B=ρ₁gh₁+ρ₂g（h'₂+h''₂），
ρ₃gh_3A+ρ₃gh_3B=ρ₁gh₁+ρ₂gh'₂+ρ₂gh''₂，
假如h_3B产生的压强和h''₂产生的压强相等，即ρ₃gh_3B=ρ₂gh''₂，
因为ρ₃＞ρ₂，所以，h_3B＜h''₂，--②
假如h_3A产生的压强和h₁、h'₂产生的压强相等，即ρ₃gh_3A=ρ₁gh₁+ρ₂gh'₂，
又因为h₁、h'₂产生的压强和h_2A、h_2B相等，
所以，ρ₃gh_3A=ρ₁gh₁+ρ₂gh'₂=ρ₂g（h_2A+h_2B），
因为，ρ₃＞ρ₂，
所以，h_3A＜h_2A+h_2B，--③
由①②③得，h_3A+h_3B+h_3C＜h_2A+h_2B+h''₂+h'₃．
所以，丙液面低于乙液面，乙液面低于甲液面．
故选D．
点评：本题考查了连通器的原理、二力平衡、液体压强，利用分割的方法、等效替代、控制变量法进行解题．