
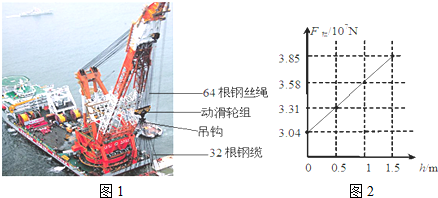
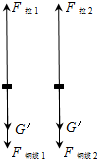
 解:
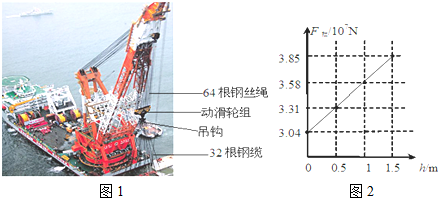
解: F拉1=
F拉1= ×3.04×107N=4.75×105N;
×3.04×107N=4.75×105N; ×100%=
×100%=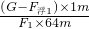 ×100%=
×100%=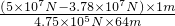 ×100%≈40.1%.
×100%≈40.1%. 求出机械效率.
求出机械效率.

科目:初中物理 来源: 题型:
 29、2007年12月22日上午,位于海面下几十米深处的“南海一号”商船被打捞浮出海面,这是中国考古史上的又一突破.“南海一号”商船长约30米,是目前发现的最大的宋代船只,如图所示.很早以前,我国考古队员就利用超声波方向性好的特点制成了一种装置安装在船上,用它发出的超声波对“南海一号”沉船进行了细致的探测.
29、2007年12月22日上午,位于海面下几十米深处的“南海一号”商船被打捞浮出海面,这是中国考古史上的又一突破.“南海一号”商船长约30米,是目前发现的最大的宋代船只,如图所示.很早以前,我国考古队员就利用超声波方向性好的特点制成了一种装置安装在船上,用它发出的超声波对“南海一号”沉船进行了细致的探测.查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
 (2008?黄浦区一模)如图是2007年12月22日“南海一号”整体打捞出海面的情景.在打捞过程中,潜水员要潜入海下将多个未充气的气囊分别均匀地安装在沉箱的四周.潜水员在海面下25米深处受到海水的压强为
(2008?黄浦区一模)如图是2007年12月22日“南海一号”整体打捞出海面的情景.在打捞过程中,潜水员要潜入海下将多个未充气的气囊分别均匀地安装在沉箱的四周.潜水员在海面下25米深处受到海水的压强为查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com