
 课外小组的同学们设计的一个用水槽来储存二次用水的冲厕装置如图所示.其中重为1N的浮球固定在横杆AB右端(B为浮球的中心),杆AB能绕O点转动,且OB是OA长度的4倍.横杆AB左端压在进水阀门C上,进水口的横截面积为4cm2.阀门C正好堵住进水口时,水箱内停止蓄水,杆AB在水平位置,且浮球浸在水中的体积为190cm3.进水口距箱底30cm,水箱内溢水管长为40cm,D是一个横截面积为30cm2的排水阀门.用金属链将排水阀门D与水箱顶部排水按钮相连,当按动排水按钮时,铁链向上拉起排水阀门D使其打开,水箱排水.要打开排水阀门D,铁链给它的拉力至少是12.5N.(进水阀门C、直杆AC、横杆AB的重力均忽略不计,进水阀门C和排水阀门D的厚度均不计,g取10N/kg).求:
课外小组的同学们设计的一个用水槽来储存二次用水的冲厕装置如图所示.其中重为1N的浮球固定在横杆AB右端(B为浮球的中心),杆AB能绕O点转动,且OB是OA长度的4倍.横杆AB左端压在进水阀门C上,进水口的横截面积为4cm2.阀门C正好堵住进水口时,水箱内停止蓄水,杆AB在水平位置,且浮球浸在水中的体积为190cm3.进水口距箱底30cm,水箱内溢水管长为40cm,D是一个横截面积为30cm2的排水阀门.用金属链将排水阀门D与水箱顶部排水按钮相连,当按动排水按钮时,铁链向上拉起排水阀门D使其打开,水箱排水.要打开排水阀门D,铁链给它的拉力至少是12.5N.(进水阀门C、直杆AC、横杆AB的重力均忽略不计,进水阀门C和排水阀门D的厚度均不计,g取10N/kg).求: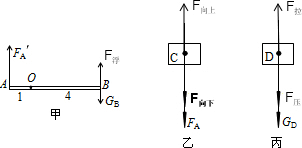
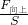 =
=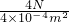 =104Pa,
=104Pa,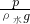 =
=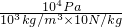 =1m,
=1m,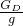 =
=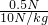 =0.05kg=50g.
=0.05kg=50g.

科目:初中物理 来源: 题型:
 (2011?石景山区二模)课外小组的同学们设计的一个用水槽来储存二次用水的冲厕装置如图所示.其中重为1N的浮球固定在横杆AB右端(B为浮球的中心),杆AB能绕O点转动,且OB是OA长度的4倍.横杆AB左端压在进水阀门C上,进水口的横截面积为4cm2.阀门C正好堵住进水口时,水箱内停止蓄水,杆AB在水平位置,且浮球浸在水中的体积为190cm3.进水口距箱底30cm,水箱内溢水管长为40cm,D是一个横截面积为30cm2的排水阀门.用金属链将排水阀门D与水箱顶部排水按钮相连,当按动排水按钮时,铁链向上拉起排水阀门D使其打开,水箱排水.要打开排水阀门D,铁链给它的拉力至少是12.5N.(进水阀门C、直杆AC、横杆AB的重力均忽略不计,进水阀门C和排水阀门D的厚度均不计,g取10N/kg).求:
(2011?石景山区二模)课外小组的同学们设计的一个用水槽来储存二次用水的冲厕装置如图所示.其中重为1N的浮球固定在横杆AB右端(B为浮球的中心),杆AB能绕O点转动,且OB是OA长度的4倍.横杆AB左端压在进水阀门C上,进水口的横截面积为4cm2.阀门C正好堵住进水口时,水箱内停止蓄水,杆AB在水平位置,且浮球浸在水中的体积为190cm3.进水口距箱底30cm,水箱内溢水管长为40cm,D是一个横截面积为30cm2的排水阀门.用金属链将排水阀门D与水箱顶部排水按钮相连,当按动排水按钮时,铁链向上拉起排水阀门D使其打开,水箱排水.要打开排水阀门D,铁链给它的拉力至少是12.5N.(进水阀门C、直杆AC、横杆AB的重力均忽略不计,进水阀门C和排水阀门D的厚度均不计,g取10N/kg).求:查看答案和解析>>
科目:初中物理 来源:北京模拟题 题型:计算题

查看答案和解析>>
科目:初中物理 来源:2012年最新经典力、热、光模拟测试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中物理 来源:2009年北京市东城区中考物理二模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com