
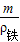 ,同理铜块受到的浮力:F铜=ρ水g
,同理铜块受到的浮力:F铜=ρ水g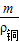 ,由于ρ铁<ρ铜,所以ρg
,由于ρ铁<ρ铜,所以ρg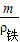 >ρ水g
>ρ水g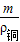 ,
,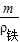 )L,同理铜块产生的力矩:(mg-ρ水g
)L,同理铜块产生的力矩:(mg-ρ水g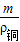 ),
),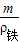 )L<(mg-ρ水g
)L<(mg-ρ水g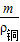 )L,
)L,

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中物理 来源: 题型:单选题
查看答案和解析>>
科目:初中物理 来源: 题型:
质量相等的铁块和铜块,分别挂在杠杆的两端,杠杆处于平衡状态,若将铜块和铁块同时浸没在水中,则杠杆( )
A. 仍保持平衡 B. 铁块一端下沉 C. 铜块一端下沉 D. 无法判断
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com