
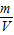
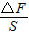 =
=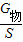 =
=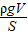 ,
,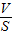 g,
g,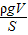 =3ρ水
=3ρ水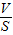 g,
g,

科目:初中物理 来源: 题型:
 (2011?长宁区一模)如图所示,水平地面上有一质量为0.1千克、容积为2.5×10-4米3的玻璃瓶,它的底面积为2.0×10-3米2,瓶内盛有0.2千克的水.一只口渴的乌鸦,为了喝到瓶内的水,将每块质量为0.01千克、密度为2.5×103千克/米3的相同的小石子投入瓶中.当水面与瓶口相平时,求:
(2011?长宁区一模)如图所示,水平地面上有一质量为0.1千克、容积为2.5×10-4米3的玻璃瓶,它的底面积为2.0×10-3米2,瓶内盛有0.2千克的水.一只口渴的乌鸦,为了喝到瓶内的水,将每块质量为0.01千克、密度为2.5×103千克/米3的相同的小石子投入瓶中.当水面与瓶口相平时,求:查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
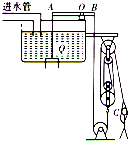 (2010?东城区二模)如图所示的是某建筑的二楼顶上的蓄水箱及放水装置,蓄水箱长3m、宽2m、高l m,楼房每层高3m.其水箱上端右侧安装了一个以O点为转轴、长为50cm的轻质杠杆AB,0点距A端40cm.A点正下方的Q是一个恰好能堵住出水口的重5N、横截面积100cm2、厚5cm的盖板,它通过细绳与杠杆的A端相连.在水箱右侧水平地面上有一质量为54.4Kg的人通过滑轮组拉动系在B点的绳子,从而控制水箱中的水从出水口流出.当水箱中蓄满水时,人用Fl的力拉绳端,盖板恰能被拉起,此时人对水平地面的压强为P1;当水箱中的水深为60cm时,人用F2的力拉绳端,盖板也恰好被拉起,此时人对水平地面的压强为P2,且P1:P2=11:12,(绳重及滑轮与轴之间的摩擦及进水管直径忽略不计,g取10N/Kg)求:
(2010?东城区二模)如图所示的是某建筑的二楼顶上的蓄水箱及放水装置,蓄水箱长3m、宽2m、高l m,楼房每层高3m.其水箱上端右侧安装了一个以O点为转轴、长为50cm的轻质杠杆AB,0点距A端40cm.A点正下方的Q是一个恰好能堵住出水口的重5N、横截面积100cm2、厚5cm的盖板,它通过细绳与杠杆的A端相连.在水箱右侧水平地面上有一质量为54.4Kg的人通过滑轮组拉动系在B点的绳子,从而控制水箱中的水从出水口流出.当水箱中蓄满水时,人用Fl的力拉绳端,盖板恰能被拉起,此时人对水平地面的压强为P1;当水箱中的水深为60cm时,人用F2的力拉绳端,盖板也恰好被拉起,此时人对水平地面的压强为P2,且P1:P2=11:12,(绳重及滑轮与轴之间的摩擦及进水管直径忽略不计,g取10N/Kg)求:查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com