

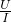 =
= =15Ω,
=15Ω, =
=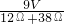 =0.18A,
=0.18A,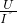 -R0=
-R0=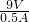 -12Ω=6Ω,
-12Ω=6Ω,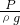 =
=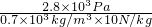 =0.4m;
=0.4m;

科目:初中物理 来源: 题型:单选题
查看答案和解析>>
科目:初中物理 来源: 题型:填空题
查看答案和解析>>
科目:初中物理 来源: 题型:解答题
 在如图所示的电路中,L1、L2分别标有“6V,3W”和“6V,6W”的字样,L3额定电压的字样看不清,而额定功率为4W清晰可见.
在如图所示的电路中,L1、L2分别标有“6V,3W”和“6V,6W”的字样,L3额定电压的字样看不清,而额定功率为4W清晰可见.查看答案和解析>>
科目:初中物理 来源: 题型:填空题
查看答案和解析>>
科目:初中物理 来源: 题型:解答题
 小明利用生活中常见的材料做了两个小实验.
小明利用生活中常见的材料做了两个小实验.查看答案和解析>>
科目:初中物理 来源: 题型:单选题
 火山爆发喷出的炽热岩浆温度可达1 200℃,岩浆流入海水中产生了大量的“白气”,如图所示.关于这些“白气”的形成是
火山爆发喷出的炽热岩浆温度可达1 200℃,岩浆流入海水中产生了大量的“白气”,如图所示.关于这些“白气”的形成是查看答案和解析>>
科目:初中物理 来源: 题型:单选题
 图所示的电路中,电源两端电压为6V并保持不变,定值电阻R1的阻值为10Ω,滑动变阻器R2的最大阻值为20Ω.当开关S闭合,滑动变阻器的滑片P由b端移到a端的过程中,下列说法中正确的是
图所示的电路中,电源两端电压为6V并保持不变,定值电阻R1的阻值为10Ω,滑动变阻器R2的最大阻值为20Ω.当开关S闭合,滑动变阻器的滑片P由b端移到a端的过程中,下列说法中正确的是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com