
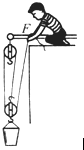
 A.某工地用如图所示的滑轮组匀速提升600N的重物,在重物上升0.2m的过程中,滑轮组的机械效率为80%(不计绳重以及滑轮轮与轴之间的摩擦,).则:
A.某工地用如图所示的滑轮组匀速提升600N的重物,在重物上升0.2m的过程中,滑轮组的机械效率为80%(不计绳重以及滑轮轮与轴之间的摩擦,).则: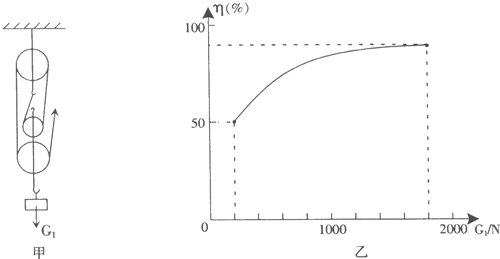

 =
=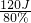 =150J;
=150J; =
=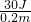 =150N;
=150N; (G物+G动)=
(G物+G动)= (750N+150N)=300N.
(750N+150N)=300N. =
=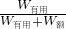 =
= =
= ,
,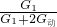
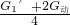 =
=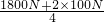 =500N;
=500N;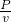 =
=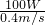 =250N,
=250N,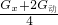
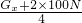
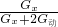 ×100%=
×100%=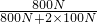 ×100%=80%.
×100%=80%. 即可求出总功的大小;
即可求出总功的大小; (G物+G动)即可求出实际拉力F.
(G物+G动)即可求出实际拉力F. =
=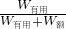 =
= =
= ,求出每一个动滑轮的重力.
,求出每一个动滑轮的重力. (G+G动)求出绳子能承受的最大拉力.
(G+G动)求出绳子能承受的最大拉力.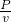 求出此时拉力的大小,然后根据F=
求出此时拉力的大小,然后根据F= (G物+G动)求出物重,最后利用η=
(G物+G动)求出物重,最后利用η= 即可求出滑轮组的实际机械效率.
即可求出滑轮组的实际机械效率. (G轮+G物)].
(G轮+G物)]. ×100%,计算相关的量,是比较常用的方法,一定要掌握.
×100%,计算相关的量,是比较常用的方法,一定要掌握. 

科目:初中物理 来源: 题型:
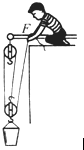 A.某工地用如图所示的滑轮组匀速提升600N的重物,在重物上升0.2m的过程中,滑轮组的机械效率为80%(不计绳重以及滑轮轮与轴之间的摩擦,).则:
A.某工地用如图所示的滑轮组匀速提升600N的重物,在重物上升0.2m的过程中,滑轮组的机械效率为80%(不计绳重以及滑轮轮与轴之间的摩擦,).则: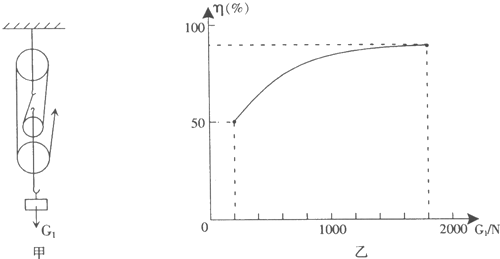
查看答案和解析>>
科目:初中物理 来源: 题型:
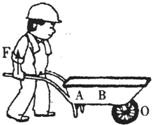 (2010?武汉模拟)建筑工地上的某工人用如图所示的小车运送一块重600N的石块,为了省力应该将石块放在A处还是B处,请在所选择的A或B处上画出石块重力的示意图,并画出工人对车施加的力F的力臂.
(2010?武汉模拟)建筑工地上的某工人用如图所示的小车运送一块重600N的石块,为了省力应该将石块放在A处还是B处,请在所选择的A或B处上画出石块重力的示意图,并画出工人对车施加的力F的力臂.查看答案和解析>>
科目:初中物理 来源:2010年湖北省武汉市部分学校五月调考物理试卷(解析版) 题型:解答题
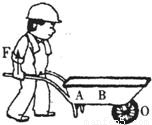
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com