
 -OA),
-OA), +OB).
+OB). -OA,由此得出OB的大小(
-OA,由此得出OB的大小( L),从而得出小木板的最远边缘到平台边缘的距离,这个距离乘以2得出D的最大距离.
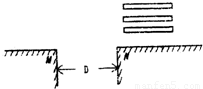
L),从而得出小木板的最远边缘到平台边缘的距离,这个距离乘以2得出D的最大距离. 解:如图,三块木板,其中两块放在平台的两边,另一块放在这两块木板上.
解:如图,三块木板,其中两块放在平台的两边,另一块放在这两块木板上. -OA,
-OA, +OB.
+OB. ×OB,
×OB, -OA,
-OA, L,小木板的最远边缘距离平台边缘为:
L,小木板的最远边缘距离平台边缘为: +OB=
+OB= +
+ =
= ,
, +OB)=2×
+OB)=2× =
= .
. 、阻力臂OB是本题的关键.
、阻力臂OB是本题的关键. 

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中物理 来源: 题型:


 ”表示平面镜),以实现上述目的.
”表示平面镜),以实现上述目的.
查看答案和解析>>
科目:初中物理 来源: 题型:
 (2012?枣庄)在课外小组里,肖英和其他同学利用木棍、铁块和细绳等材料制作了一杆可以测量液体密度的“密度秤”.把细绳系在木棍的重心O处并把木棍挂起,如图所示,M和N是两个铁块.当M在A点,N在B点时,木棍如图所示平衡.把M浸没在水中,N移至C点时,木棍再次水平平衡.把M浸没在某种液体中,N移至D点时,木棍又处于水平平衡.可知被测液体的密度与水的密度关系是( )
(2012?枣庄)在课外小组里,肖英和其他同学利用木棍、铁块和细绳等材料制作了一杆可以测量液体密度的“密度秤”.把细绳系在木棍的重心O处并把木棍挂起,如图所示,M和N是两个铁块.当M在A点,N在B点时,木棍如图所示平衡.把M浸没在水中,N移至C点时,木棍再次水平平衡.把M浸没在某种液体中,N移至D点时,木棍又处于水平平衡.可知被测液体的密度与水的密度关系是( )查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,M、N是两个等高的平台,两平台相距D.现用三块质量均匀、质量和形状完全相同的长方形木块在M、N之间搭成水平梁,已知每块木板的长为L,则M、N两平台间允许的最大距离为多少?请画出示意图,并简要说明理由.
如图所示,M、N是两个等高的平台,两平台相距D.现用三块质量均匀、质量和形状完全相同的长方形木块在M、N之间搭成水平梁,已知每块木板的长为L,则M、N两平台间允许的最大距离为多少?请画出示意图,并简要说明理由.查看答案和解析>>
科目:初中物理 来源: 题型:
 如图所示,M、N是两接线柱,当M接C、N接B时,闭合开关S后,为了使小灯泡变亮,滑片P应向
如图所示,M、N是两接线柱,当M接C、N接B时,闭合开关S后,为了使小灯泡变亮,滑片P应向查看答案和解析>>
科目:初中物理 来源: 题型:解答题


 ”表示平面镜),以实现上述目的.
”表示平面镜),以实现上述目的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com