20
分析:本题有4个过程,画出每一个过程的电路图.
(1)当开关S
1、S
2都断开时,滑动变阻器在b端时,灯泡L和滑动变阻器的整个电阻R
ab串联在电路中,电路电流为I
甲,如图甲.
(2)当开关S
1、S
2都断开时,滑动变阻器R的滑片P从b端滑到某一位置c时,如图乙.
滑动变阻器R
ab接入电路的电阻减小6Ω,电源电压不变,总电阻减小,电流增大,I
乙=I
甲+0.1A,此时灯泡正常工作,根据灯泡的额定电压和额定功率,求出乙图中的电流.可以求出甲图中的电流.
根据甲乙两个过程的电源电压相等列出等式,求出滑动变阻器的最大阻值R
ab、R
ac、电源电压U.
(3)保持滑动变阻器滑片P的位置不变,闭合开关S
1、S
2,灯泡被短路,R
0与R
ac并联,如图丙,总电阻减小,干路电流增大,干路电流为I
丙=I
乙+1.5A.由总电压和总电流求出总电阻,求出R
0的电阻.
(4)闭合开关S
1、S
2,R
0与滑动变阻器并联,要使电路功率最小,电源电压一定,电路总电流最小,总电阻最大,R
0是定值电阻,滑动变阻器连入电路的阻值最大时,电路总电阻最大,如图丁,求各支路电流,求总电流,求出消耗的最小功率.
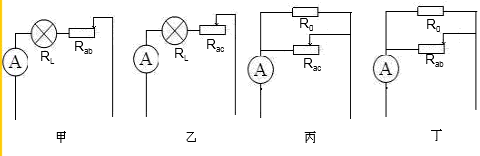
解答:甲图:当开关S
1、S
2都断开时,灯泡L和滑动变阻器的整个电阻R
ab串联在电路中,电路电流为I
甲.
乙图:当开关S
1、S
2都断开时,滑片滑到c处,灯泡L和滑动变阻器的R
ac串联,电路电阻减小,电流增大,I
乙=I
甲+0.1A,
此时灯泡正常工作,I
乙=
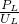
=
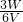
=0.5A,
I
甲=I
乙-0.1A=0.5A-0.1A=0.4A,
灯泡电阻为:R
L=
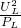
=
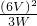
=12Ω,
根据甲乙两个过程电源电压相等,所以,I
甲R
甲=I
乙R
乙,
I
甲(R
L+R
ab)=I
乙(R
L+R
ac),
I
甲(R
L+R
ab)=I
乙(R
L+R
ab-6Ω),
0.4A×(12Ω+R
ab)=0.5A×(12Ω+R
ab-6Ω),
所以,R
ab=18Ω,R
ac=12Ω,
U=I
甲(R
L+R
ab)=0.4A×(12Ω+18Ω)=12V.
丙图:保持滑动变阻器滑片P的位置不变,闭合开关S
1、S
2,灯泡被短路,R
0与R
ac并联,总电阻减小,电源电压不变,总电流增大,
I
丙=I
乙+1.5A=0.5A+1.5A=2A,
所以,电路总电阻为:R
丙=
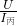
=
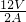
=6Ω,
R
丙=
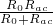
,
6Ω=
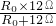
,
所以,R
0=12Ω.
丁图:当开关S
1、S
2都闭合时,R
0与滑动变阻器并联,要使总功率最小,电源电压一定,电路总电流最小,总电阻最大,滑动变阻器电阻最大,电路总电阻最大,所以,R
0与R
ab并联,
I
0=
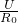
=
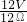
=1A,
I
ab=
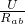
=
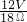
=

A,
所以,I
丁=I
0+I
ab=1A+

A=

A,
P
丁=UI
丁=12V×

A=20W.
故答案为:20.
点评:本题属于比较难的电学计算题,本题通过开关的闭合与断开,滑动变阻器的滑片变化来完成电路的不同过程,针对此类习题,需要弄清几个过程,有几个过程,画几个电路图,找各个过程的不变量,把几个过程联系起来.不同过程电源电压相等是常见的一种方法,此方法即简单,又常用,又典型.

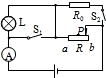 在如图所示的电路中,灯泡L标有“6V 3W”字样,电源两端的电压和灯丝的电阻均保持不变.当开关S1、S2都断开时,滑动变阻器R的滑片P从b端滑到某一位置c时(图中未标出),滑动变阻器R接入电路的电阻减小6Ω,电流表示数变化了0.1 A,灯泡恰好正常发光.保持滑动变阻器滑片P的位置不变,闭合开关S1、S2,电流表示数又变化了1.5A.当开关S1、S2都闭合时,调节滑动变阻器滑片P的位置(滑片P不接触a端),电路消耗的总功率的最小值为________W.
在如图所示的电路中,灯泡L标有“6V 3W”字样,电源两端的电压和灯丝的电阻均保持不变.当开关S1、S2都断开时,滑动变阻器R的滑片P从b端滑到某一位置c时(图中未标出),滑动变阻器R接入电路的电阻减小6Ω,电流表示数变化了0.1 A,灯泡恰好正常发光.保持滑动变阻器滑片P的位置不变,闭合开关S1、S2,电流表示数又变化了1.5A.当开关S1、S2都闭合时,调节滑动变阻器滑片P的位置(滑片P不接触a端),电路消耗的总功率的最小值为________W.
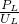 =
=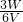 =0.5A,
=0.5A,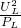 =
=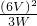 =12Ω,
=12Ω,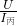 =
=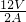 =6Ω,
=6Ω,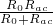 ,
,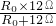 ,
,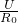 =
=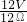 =1A,
=1A,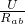 =
=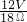 =
= A,
A, A=
A= A,
A, A=20W.
A=20W.

 (2011?杨浦区二模)在如图所示的电路中,电源电压保持不变,当电键S由断开到闭合时,电压表V的示数将
(2011?杨浦区二模)在如图所示的电路中,电源电压保持不变,当电键S由断开到闭合时,电压表V的示数将 (2012?南通模拟)在如图所示的电路中,R1=10Ω,R2=20Ω,闭合开关后,电流表的示数为0.3A.求:
(2012?南通模拟)在如图所示的电路中,R1=10Ω,R2=20Ω,闭合开关后,电流表的示数为0.3A.求: