B
分析:画出示意图,原来杠杆处于平衡状态,两边的力和力臂的乘积相等,得出ρ
铝v
1g×OA=ρ
铁v
2g×OB;
把铝块和铁块的两端同时浸入水中,铝块和铁块受到水的浮力,先得出两边浮力和力臂乘积的关系,再推导此时两边受拉力和力臂的乘积关系,得出向哪端倾斜.
解答:
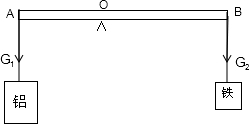
解:如上图,杠杆两端分别挂着不同质量的铝块和铁块,杠杆处于平衡状态,
G
1×OA=G
2×OB,
∵G=mg=ρvg,
∴ρ
铝v
1g×OA=ρ
铁v
2g×OB,--------------①
∵ρ
铝<ρ
铁,
∴v
1g×OA>v
2g×OB;
把铝块和铁块的两端同时浸入水中,
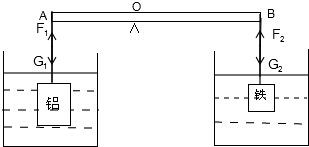
如下图,
A端受力F
A=G
1-F
1=ρ
铝v
1g-ρ
水v
1g,
B端受力F
B=G
2-F
2=ρ
铁v
2g-ρ
水v
2g,
F
A×OA=ρ
铝v
1g×OA-ρ
水v
1g×OA,
F
B×OB=ρ
铁v
2g×OB-ρ
水v
2g×OB,
∵v
1g×OA>v
2g×OB,
∴ρ
水v
1g×OA>ρ
水v
2g×OB,-------------------②
由①②得:
ρ
铝v
1g×OA-ρ
水v
1g×OA<ρ
铁v
2g×OB-ρ
水v
2g×OB,
即:F
A×OA<F
B×OB,
∴铁的一端下降
故选B.
点评:本题关键:一画出杠杆示意图帮助分析,二是分析得出两边浮力和力臂乘积的大小关系.

 解:如上图,杠杆两端分别挂着不同质量的铝块和铁块,杠杆处于平衡状态,
解:如上图,杠杆两端分别挂着不同质量的铝块和铁块,杠杆处于平衡状态, 如下图,
如下图,

 阅读快车系列答案
阅读快车系列答案