
 如图1所示将边长为10cm的密度均匀的正方体木块平放在圆柱形容器的底部,圆柱形容器的横截面积为300cm2,此时正方体木块对圆柱形容器的底部的压强是800N/m2.现缓慢地往容器中注水,当容器中的水面升至一定高度时,木块对容器底面的压力恰好为零,如图2所示.已知g=10N/kg,ρ水=1.0×103kg/m3.求:
如图1所示将边长为10cm的密度均匀的正方体木块平放在圆柱形容器的底部,圆柱形容器的横截面积为300cm2,此时正方体木块对圆柱形容器的底部的压强是800N/m2.现缓慢地往容器中注水,当容器中的水面升至一定高度时,木块对容器底面的压力恰好为零,如图2所示.已知g=10N/kg,ρ水=1.0×103kg/m3.求: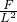 ,可得F=PL2=800N/m2×100×10-4m2=8N,
,可得F=PL2=800N/m2×100×10-4m2=8N,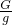 =
= =0.8kg.
=0.8kg.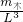 =
=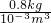 =0.8×103 kg/m3.
=0.8×103 kg/m3. 可求得木块的密度.
可求得木块的密度.

科目:初中物理 来源: 题型:
 (2011?咸宁)如图1所示将边长为10cm的密度均匀的正方体木块平放在圆柱形容器的底部,圆柱形容器的横截面积为300cm2,此时正方体木块对圆柱形容器的底部的压强是800N/m2.现缓慢地往容器中注水,当容器中的水面升至一定高度时,木块对容器底面的压力恰好为零,如图2所示.已知g=10N/kg,ρ水=1.0×103kg/m3.求:
(2011?咸宁)如图1所示将边长为10cm的密度均匀的正方体木块平放在圆柱形容器的底部,圆柱形容器的横截面积为300cm2,此时正方体木块对圆柱形容器的底部的压强是800N/m2.现缓慢地往容器中注水,当容器中的水面升至一定高度时,木块对容器底面的压力恰好为零,如图2所示.已知g=10N/kg,ρ水=1.0×103kg/m3.求:查看答案和解析>>
科目:初中物理 来源:2011-2012学年湖北省襄阳市枣阳市熊集中学九年级(上)期末物理试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中物理 来源:2012年广西北海市合浦县中考物理模拟试卷(4月份)(解析版) 题型:解答题

查看答案和解析>>
科目:初中物理 来源:2011年湖北省咸宁市中考物理试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com