
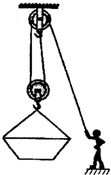
 某建筑工地用如图所示的简易滑轮组将重4000N的砖块运到离地4m高的砌墙处,已知每个滑轮重100N,滑轮摩擦和绳重以及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为500N,求:
某建筑工地用如图所示的简易滑轮组将重4000N的砖块运到离地4m高的砌墙处,已知每个滑轮重100N,滑轮摩擦和绳重以及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为500N,求: ×100%=
×100%=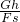 =
= =
=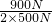 =90%;
=90%; ≈4.4,故需要5次搬完;
≈4.4,故需要5次搬完; (G砖+G轮).
(G砖+G轮). 

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中物理 来源: 题型:
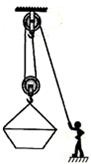 某建筑工地用如图所示的简易滑轮组将重4000N的砖块运到离地4m高的砌墙处,已知每个滑轮重100N,滑轮摩擦和绳重以及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为500N,求:
某建筑工地用如图所示的简易滑轮组将重4000N的砖块运到离地4m高的砌墙处,已知每个滑轮重100N,滑轮摩擦和绳重以及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为500N,求:查看答案和解析>>
科目:初中物理 来源: 题型:
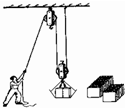 (2012?连云港二模)某建筑工地用如图所示的简易滑轮组将重3400N的砖块运到离地4m高的砌墙处.已知每个滑轮重100N,轮与轴的摩擦、绳重及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为400N,求:
(2012?连云港二模)某建筑工地用如图所示的简易滑轮组将重3400N的砖块运到离地4m高的砌墙处.已知每个滑轮重100N,轮与轴的摩擦、绳重及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为400N,求:查看答案和解析>>
科目:初中物理 来源: 题型:
 (2012?太仓市一模)某建筑工地用如图所示的简易滑轮组将重4000N的砖块运到离地4m高的砌墙处,已知每个滑轮重100N,滑轮摩擦和绳重以及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为500N,求:
(2012?太仓市一模)某建筑工地用如图所示的简易滑轮组将重4000N的砖块运到离地4m高的砌墙处,已知每个滑轮重100N,滑轮摩擦和绳重以及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为500N,求:查看答案和解析>>
科目:初中物理 来源: 题型:
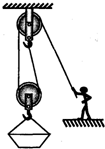 某建筑工地用如图所示的简易滑轮组将重4000N的砖块运到离地4m高的砌墙处,已知每个滑轮重100N,滑轮摩擦和绳重以及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为500N,求:
某建筑工地用如图所示的简易滑轮组将重4000N的砖块运到离地4m高的砌墙处,已知每个滑轮重100N,滑轮摩擦和绳重以及动滑轮下的挂网重忽略不计.若提升砖块的工人作用于绳的拉力最大为500N,求:查看答案和解析>>
科目:初中物理 来源: 题型:
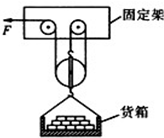 某建筑工地用如图所示升降机来提升实心砖.升降机货箱的重力是400N,每个滑轮中50N,不计钢丝绳的重力和摩擦.g取10N/kg.试求:
某建筑工地用如图所示升降机来提升实心砖.升降机货箱的重力是400N,每个滑轮中50N,不计钢丝绳的重力和摩擦.g取10N/kg.试求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com