
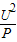 可求灯泡的电阻,再利用公式P=I2R可求两灯消耗的实际功率,
可求灯泡的电阻,再利用公式P=I2R可求两灯消耗的实际功率,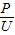 求出各自的额定电流,电路两端允许加的最大电压就等于串联电阻之和与最小电流的乘积.
求出各自的额定电流,电路两端允许加的最大电压就等于串联电阻之和与最小电流的乘积.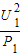 =
=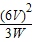 =12Ω,L2的电阻R2=
=12Ω,L2的电阻R2=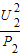 =
=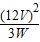 =48Ω,
=48Ω,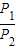 =
=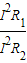 =
=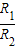 =
=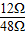 =
= ,
,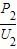 =
=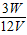 =0.25A,
=0.25A,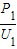 =
=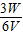 =0.5A,
=0.5A,

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源:2012-2013学年北京市昌平区九年级(上)期末物理试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com