质量为68g的空瓶子,装满水后的总质量为184g,若先在瓶中放入36g的金属块,然后再装满水,发现总质量为216g,则瓶子的容积为 m3,此金属块的密度为 kg/m3.
【答案】
分析:(1)已知空瓶子的质量和装满水后的总质量可求所装水的质量,根据密度公式求出水的体积即为瓶子的容积;
(2)瓶子放入金属块后再装满水时,用总质量减掉瓶子和金属块的质量即为所装水的质量,根据密度公式求出此时水的体积,瓶子的容积减掉水的体积即为金属块的体积,然后用金属块的质量除以金属块的体积即可求出金属块的密度.
解答:解:(1)瓶子装满水时,水的质量:
m
水=m
总-m
瓶=184g-68g=116g,
瓶子的容积:
V=V
水=

=

=116cm
3=1.16×10
-4m
3;
(2)瓶子放入金属块后再装满水时,水的质量:
m
水′=m
总-m
金-m
瓶=216g-36g-68g=112g,
水的体积:
V
水´=

=
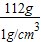
=112cm
3,
金属块的体积:
V
金=V-V
水´=116cm
3-112cm
3=4cm
3,
金属块的密度:
ρ
金=

=
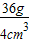
=9g/cm
3=9×10
3kg/m
3.
故答案为:1.16×10
-4;9×10
3.
点评:本题考查密度的计算,关键是知道空瓶子的容积等于空瓶子装满水后水的体积以及金属块的体积等于瓶子的容积减掉水的体积,解题过程要注意单位的灵活应用.

 =
= =116cm3=1.16×10-4m3;
=116cm3=1.16×10-4m3; =
=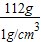 =112cm3,
=112cm3, =
=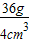 =9g/cm3=9×103kg/m3.
=9g/cm3=9×103kg/m3.
