
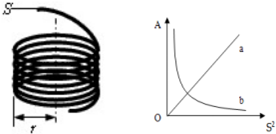
 归纳是探究:
归纳是探究:| 实验 | 材料 | S/m2 | n/匝 | r/m | A(N•m-1) |
| 1 | 铜 | 3×10-6 | 100 | 1×10-2 | 90 |
| 2 | 钢 | 3×10-6 | 100 | 1×10-2 | 180 |
| 3 | 铜 | 6×10-6 | 100 | 1×10-2 | 360 |
| 4 | 钢 | 3×10-6 | 200 | 1×10-2 | 90 |
| 5 | 铜 | 6×10-6 | 100 | 2×10-2 | 45 |
分析 (1)实验中主要有四个变量,分别为材料、横截面积、弹簧匝数和弹簧的半径,根据控制变量法的要求,分别比较实验1、3数据,实验3、5数据,可分析出横截面积、弹簧的半径与A的关系,再利用前面求得的横截面积与A的关系式,求得当实验1中的横截面积变为和实验4中的横截面积相同的A,与实验4进行比较得出弹簧匝数与A的关系,最终归纳出表达式,并利用表达式计算出铜的k值;
(2)通过刚性系数的表达式,可以看出,弹簧的刚性系数和和横截面积为正比例函数关系,因此,a是符合题意的;
(3)通过表格可以看出铜与钢谁的刚性系数更大,再根据相同条件下,刚性系数越大的弹簧越难被拉伸这一规律可做出判断;
(4)利用归纳得出的公式求出钢制造的弹簧的k值,将数据代入进行计算可得出该弹簧的匝数.
解答 解:(1)由题意和表格可知,弹簧的刚性系数A与制造弹簧的金属丝的材料、金属丝的横截面积S、弹簧的匝数n、弹簧的半径r有关;
①根据控制变量法,要研究弹簧的刚性系数A与制造弹簧的金属丝的横截面积S的关系,要使制造弹簧的材料、弹簧的匝数n、弹簧的半径r相同,改变金属丝的横截面积S,应选择表格中的实验1、实验3,
分析数据可知,实验1中金属丝的横截面积S为3×10-6m2,实验3中金属丝的横截面积S为6×10-6m2,实验3中金属丝的横截面积是实验1中金属丝的横截面积的2倍,
弹簧的刚性系数A由90N•m-1变为360N•m-1,实验3中弹簧的刚性系数是实验1中弹簧的刚性系数的4倍,
则当其他因素相同时,弹簧的刚性系数A与金属丝的横截面积S的关系可表示为A=k1S2;
②根据控制变量法,要研究弹簧的刚性系数A与弹簧的半径r的关系,要使制造弹簧的材料、金属丝的横截面积S、弹簧的匝数n,改变弹簧的半径r,应选择表格中的实验3、实验5,
分析数据可知,实验3中弹簧的半径r为1×10-2m,实验3中弹簧的半径r为2×10-2m,实验5中弹簧的半径r是实验3中弹簧的半径r的2倍,
弹簧的刚性系数A由360N•m-1变为45N•m-1,实验5中弹簧的刚性系数是实验3中弹簧的刚性系数的$\frac{1}{8}$,
则当其他因素相同时弹簧的刚性系数A与弹簧的半径r的关系可表示为A=k2 $\frac{1}{{r}^{3}}$;
③分析实验2,若其他因素保持不变,S由3×10-6m2增大为原来的两倍变为6×10-6m2,根据①中推导出的则当其他因素相同时,弹簧的刚性系数A与金属丝的横截面积S的关系表示式A=k1S2可知,弹簧的刚性系数A应由由180N•m-1增大为原来的4倍变为720N•m-1,
即可得到如下数据:钢制造弹簧的金属丝的横截面积S为6×10-6m2,弹簧的匝数n为100,弹簧的半径r为1×10-2m,弹簧的刚性系数为720N•m-1,
实验4与以上数据比较,其他因素保持不变,弹簧的匝数n有原来的100变为实验4中的200,为原来的2倍,弹簧的刚性系数A由720N•m-1变为360N•m-1,变为原来的$\frac{1}{2}$,则当其他因素相同时弹簧的刚性系数A与弹簧的匝数n的关系可表示为A=k3 $\frac{1}{n}$;
综合①②③可知,弹簧的刚性系数A的表达式为A=k$\frac{{S}^{2}}{n{r}^{3}}$;
取任意一组铜制造的弹簧的实验数据代入弹簧的刚性系数A的表达式,以实验1数据代入为例,
90N/m=k铜 $\frac{(3×1{0}^{-6}{m}^{2})^{2}}{100×(1×1{0}^{-2}m)^{3}}$,解得k铜=109N/m2;
(2)用粗细不同的铜丝做成半径相同和匝数都相同的弹簧,由(1)③可知,弹簧的刚性系数和横截面积的关系式为A=k3 $\frac{1}{n}$,为反正例函数关系,可以用如图中的图线a表示;
(3)比较实验数据1、2,当金属丝的横截面积S、弹簧的匝数n、弹簧的半径r均相同时,铜的刚性系数小于钢的刚性系数,
即用粗细相同的铜丝和钢丝做成匝数和半径相同的弹簧,都用10N的力拉伸时,用铜做成的弹簧变得更长;
(4)由(1)可知,弹簧的刚性系数A的表达式为A=k$\frac{{S}^{2}}{n{r}^{3}}$,
取任意一组钢制造的弹簧的实验数据代入弹簧的刚性系数A的表达式,以实验2数据代入为例,
180N/m=k铜 $\frac{(3×1{0}^{-6}{m}^{2})^{2}}{100×(1×1{0}^{-2}m)^{3}}$,解得k钢=2×109N/m2,
则钢制造的弹簧的刚性系数A的表达式为A=2×109N/m2 $\frac{{S}^{2}}{n{r}^{3}}$,
将数据代入得,100N/m=2×109N/m2 $\frac{{(2×1{0}^{-6}{m}^{2})}^{2}}{n(1×1{0}^{-2}m)^{3}}$,
解得,n=80.
故答案为:(1)$\frac{{S}^{2}}{n{r}^{3}}$;109N/m2;(2)a;(3)铜;(4)80.
点评 本实验中的变量比较多,在分析数据时,必须在保证其他变量不变的情况下,依次分析其中的一个变量与刚性系数之间的关系,最终综合成公式的形式,有了刚性系数的公式,剩余的问题基本要从公式入手进行分析和计算,本题的难点在于当有两个变量均改变时,如何研究其中的一个变量与刚性系数之间的关系,我们可以通过前面的关系式,推导得出一组新的只有一个变量改变的实验数据再进行分析比较.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中物理 来源: 题型:实验探究题
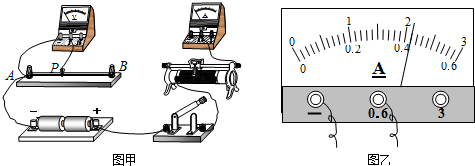
| l/cm | 30 | 40 | 50 | 60 | 70 | 80 |
| R/Ω | 2.1 | 2.8 | 3.5 | 4.2 | 4.9 | 5.6 |
查看答案和解析>>
科目:初中物理 来源: 题型:实验探究题
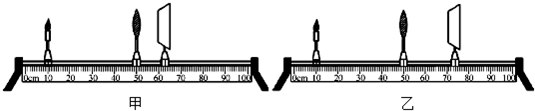
查看答案和解析>>
科目:初中物理 来源: 题型:填空题
查看答案和解析>>
科目:初中物理 来源: 题型:选择题
| A. | 将橡皮泥捏成各种形状的小动物 | B. | 撑杆跳高运动员将撑杆压弯 | ||
| C. | 抛出的铅球会落回地面 | D. | 将弹簧拉力器拉开 |
查看答案和解析>>
科目:初中物理 来源: 题型:填空题
 2016年3月15日下午4点,埃及航空公司一波音373-800飞机在即将到达伦敦西斯罗机场时,被一只鸟猛烈撞击,飞机前部被严重破坏,如图所示,上述现象表明力可以改变物体的形状,在此过程中,飞机撞小鸟的力等于小鸟撞飞机的力(选填“大于”“小于”或“等于”).
2016年3月15日下午4点,埃及航空公司一波音373-800飞机在即将到达伦敦西斯罗机场时,被一只鸟猛烈撞击,飞机前部被严重破坏,如图所示,上述现象表明力可以改变物体的形状,在此过程中,飞机撞小鸟的力等于小鸟撞飞机的力(选填“大于”“小于”或“等于”).查看答案和解析>>
科目:初中物理 来源: 题型:填空题
 人们在生活中用热水取暖,在生产上常用水作为冷却剂,这主要是因为水的比热容 较大.如图所示,锤头松动时,用力敲锤柄是利用惯性使锤头套紧;如果长时间看手机、玩电子游戏,容易造成眼睛近视.矫正近视眼,应该佩戴镜片是凹透镜的眼镜.
人们在生活中用热水取暖,在生产上常用水作为冷却剂,这主要是因为水的比热容 较大.如图所示,锤头松动时,用力敲锤柄是利用惯性使锤头套紧;如果长时间看手机、玩电子游戏,容易造成眼睛近视.矫正近视眼,应该佩戴镜片是凹透镜的眼镜.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com