
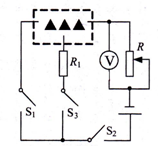
 如图所示,电源电压为6V,R为“30Ω,0.25A”滑动变阻器,R1为“10Ω,0.4A”电阻,电压表量程为0-3V.图中虚线框内接一只“20Ω,0.3A”电阻R2(未画出).已知:①闭合S1和S2,断开S3时,调节R,使其接入电路的阻值为10Ω,此时电路消耗的电功率为1.2W;②断开S1,闭合S2、S3,调节R,使其接入电路的阻值为6Ω,此时电压表的示数为1.0V.
如图所示,电源电压为6V,R为“30Ω,0.25A”滑动变阻器,R1为“10Ω,0.4A”电阻,电压表量程为0-3V.图中虚线框内接一只“20Ω,0.3A”电阻R2(未画出).已知:①闭合S1和S2,断开S3时,调节R,使其接入电路的阻值为10Ω,此时电路消耗的电功率为1.2W;②断开S1,闭合S2、S3,调节R,使其接入电路的阻值为6Ω,此时电压表的示数为1.0V. 可得,在情形①中电路的总阻值:
可得,在情形①中电路的总阻值: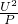 =
= =30Ω;
=30Ω;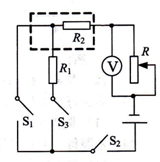
 =
=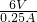 =24Ω,
=24Ω,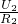 =
=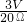 =0.15A,
=0.15A,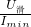 =
= =20Ω,
=20Ω, 求出电路的总阻值;
求出电路的总阻值;

科目:初中物理 来源: 题型:
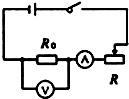 如图所示,电源电压为6V且保持不变,滑动变阻器的最大阻值为20?,定值电阻R0为5?.闭合开关后,移动滑片,发现能使电流表(“0~0.6A”或“0~3A”)和电压表(“0~3V”或“0~15V”)的指针同时达到满刻度线.则R0的电功率与电流的关系图象可能是( )
如图所示,电源电压为6V且保持不变,滑动变阻器的最大阻值为20?,定值电阻R0为5?.闭合开关后,移动滑片,发现能使电流表(“0~0.6A”或“0~3A”)和电压表(“0~3V”或“0~15V”)的指针同时达到满刻度线.则R0的电功率与电流的关系图象可能是( )A、 | B、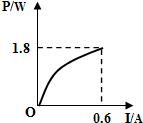 | C、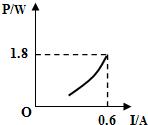 | D、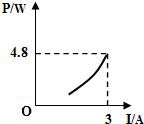 |
查看答案和解析>>
科目:初中物理 来源: 题型:
 (2013?徐州模拟)如图所示,电源电压为6V,R1阻值为10Ω,R2阻值为20Ω.R1与R2的连接方式为
(2013?徐州模拟)如图所示,电源电压为6V,R1阻值为10Ω,R2阻值为20Ω.R1与R2的连接方式为查看答案和解析>>
科目:初中物理 来源: 题型:
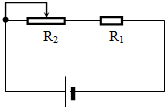 如图所示,电源电压为8V,R1=4Ω,滑动变阻器的最大阻值是12Ω,滑片滑到左端时,通过R1的电流为
如图所示,电源电压为8V,R1=4Ω,滑动变阻器的最大阻值是12Ω,滑片滑到左端时,通过R1的电流为查看答案和解析>>
科目:初中物理 来源: 题型:
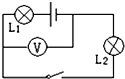 如图所示,电源电压为6V且保持不变.当开关闭合时,电压表的示数为2V,则:
如图所示,电源电压为6V且保持不变.当开关闭合时,电压表的示数为2V,则:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com