
 为了研究在已装有物体的容器中加入水后,容器对桌面压强的增加量△p桌、水对容器底部压强的增加量△p水与哪些因素有关,某同学先在足够高的薄壁圆柱型容器底放入一个铝质实心圆柱体后再倒入一定体积的水,如图所示.并分别测出了每次△p桌、△p液,实验数据记录在表中.
为了研究在已装有物体的容器中加入水后,容器对桌面压强的增加量△p桌、水对容器底部压强的增加量△p水与哪些因素有关,某同学先在足够高的薄壁圆柱型容器底放入一个铝质实心圆柱体后再倒入一定体积的水,如图所示.并分别测出了每次△p桌、△p液,实验数据记录在表中.| 实验序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 倒入水的体积V/m3 | 0 | 0.002 | 0.004 | 0.006 | 0.008 | 0.010 | 0.012 | 0.014 | 0.016 |
| △p桌/Pa | 0 | 2000 | 4000 | 6000 | 8000 | 10000 | 12000 | 14000 | 16000 |
| △p水/Pa | 0 | 4000 | 8000 | 12000 | 16000 | 19000 | 21000 | 23000 | 25000 |
分析 ①分析压强的增加量与水的体积的变化,得出正比例关系;
②分析表中数据得出压强增加量与倒入水的体积V的关系;
③分析表格中数据,看水对容器底部压强的增加量与体积增加量的关系,得出结论;
④综合分析表中数据,比较圆柱体在浸没前后水对容器底部压强的增加量的变化情况,可判断其深度的变化情况,进而推理得出圆柱体的底面积是圆柱型容器底面积的关系;
根据压强的公式p=ρgh可求出当圆柱体浸没后水的深度;再利用公式p=ρgh=ρg$\frac{V}{S}$计算圆柱形容器的底面积,以及浸没后水和圆柱体的总体积,再减去水的体积,即可得出圆柱体的体积.
解答 解:
①分析比较表第二行和第三行数据可得出水的体积增加,液体压强增加量也增大,且液体压强增加量与水的体积增加量的比值不变,可知:△p桌与倒入水的体积V成正比;
②分析比较表第二行和第四行,倒入水的体积V与水对容器底部压强的增加量△p水,可得出初步结论是倒入水的体积越大,水对容器底部压强的增加量△p水越大;
③分析表中数据可知,当倒入水的体积≤0.008m3时,水的体积每增加0.002m3,水对容器底部压强的增加量△p水增加4000Pa,而当倒入水的体积≥0.010m3时,水的体积每增加0.002m3,水对容器底部压强的增加量△p水增加2000Pa,说明圆柱体在这一范围内刚好被倒入的水浸没.故A符合题意.
④综合分析表中数据,由上述分析可知,实验序号5之前,圆柱体未浸没,实验序号6之后,圆柱体浸没了,在圆柱体浸没前后,水对容器底部压强的变化量减小了一半,由公式可得:p=ρgh=ρg$\frac{V}{S}$,压强p减小一半,是底面积S增大了一倍所致,因此可得,圆柱型容器底面积是圆柱体底面积的2倍,即圆柱体的底面积是圆柱型容器底面积的0.5倍;
以第6次实验为例,当圆柱体完全浸没后,由p=ρgh得,
水的深度h=$\frac{p}{ρg}$=$\frac{19000Pa}{1.0×1{0}^{3}kg/{m}^{3}×10N/kg}$=1.9m;
以第6-7次实验的变化为例,圆柱体浸没后△p水=ρg△h=ρg$\frac{△V}{S}$,
代入数据得,21000Pa-19000Pa=1.0×103kg/m3×10N/kg×$\frac{0.012{m}^{3}-0.010{m}^{3}}{S}$,
解得容器的底面积S=0.01m2,
在第6次实验中,水和圆柱体的总体积:V总=Sh=0.01m2×1.9m=0.019m3;
则圆柱体的体积V圆柱体=V总-V水=0.019m3-0.010m3=0.009m3.
故答案为:①成正比;②倒入水的体积越大,水对容器底部压强的增加量△p水越大;
③A;④0.5;0.009.
点评 此题是探究物体在浸入液体中的过程中,底部压强增加量与水的体积增加量之间的关系,要学习分析数据的方法,并注意控制变量法的应用.
此题的难点是结合表中数据的变化关系,利用液体压强的公式和圆柱体的公式,求出圆柱体的体积,有一定难度.


科目:初中物理 来源: 题型:实验探究题
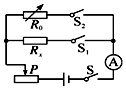 (1)电阻箱Ro可以看成是阻值已知的定值电阻(如图),小明利用该电路测未知电阻Rx,做法如下:闭合开关S、S1,调节滑片P,使电流表读数I,然后再断开S1,闭合S2,调节Ro,使电流表示数仍为I,则待测电阻Rx=此时电阻厢连入电路中的电阻大小.
(1)电阻箱Ro可以看成是阻值已知的定值电阻(如图),小明利用该电路测未知电阻Rx,做法如下:闭合开关S、S1,调节滑片P,使电流表读数I,然后再断开S1,闭合S2,调节Ro,使电流表示数仍为I,则待测电阻Rx=此时电阻厢连入电路中的电阻大小.查看答案和解析>>
科目:初中物理 来源: 题型:多选题
| A. | 比热容是物质自身的性质,与质量,状态,吸收或放出的热量均无关 | |
| B. | 相同质量的铝和铜,吸收了相同的热量,铝上升的温度高(C铝>C铜) | |
| C. | 沿海地区昼夜温差较小,而内陆沙漠地区的昼夜温差较大,这主要是因为海水吸收的热量少,砂石吸收的热量多 | |
| D. | 我国北方楼房中的“暖气”用水作为介质是利用水的比热容大 |
查看答案和解析>>
科目:初中物理 来源: 题型:计算题
查看答案和解析>>
科目:初中物理 来源: 题型:实验探究题
 小霞在学习了电学知识后,认为:在串联电路中,定值电阻阻值不变,它两端的电压就不变.请你利用如图所示器材设计一个实验证明她的观点是错误的.
小霞在学习了电学知识后,认为:在串联电路中,定值电阻阻值不变,它两端的电压就不变.请你利用如图所示器材设计一个实验证明她的观点是错误的.查看答案和解析>>
科目:初中物理 来源: 题型:填空题
查看答案和解析>>
科目:初中物理 来源: 题型:实验探究题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com