
 ,可求出两球的体积比.
,可求出两球的体积比.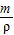 ,所以两球体积比
,所以两球体积比 =
= =
= =
= =
= ,根据阿基米德原理F浮=G排=ρ液gV排,可知:F甲:F乙=V甲:V乙=1:3,故选项A不合题意.
,根据阿基米德原理F浮=G排=ρ液gV排,可知:F甲:F乙=V甲:V乙=1:3,故选项A不合题意. ,F乙浮=ρ水g
,F乙浮=ρ水g  ,
, ,F乙=G-F乙浮=mg-ρ水g
,F乙=G-F乙浮=mg-ρ水g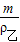 ,
, =
=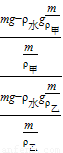 =
= ?
?
 ?
? =
= ,故选项B符合题意.
,故选项B符合题意.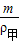 ,V乙=
,V乙=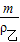 ,
,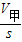 =
=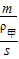 ,△hB=
,△hB= =
= ,
,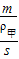 =
= ,
,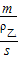 =
=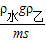 ,
, =
= =
= =
= =
= .故选项C符合题意.
.故选项C符合题意.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
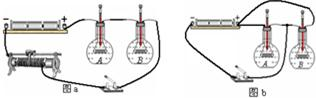
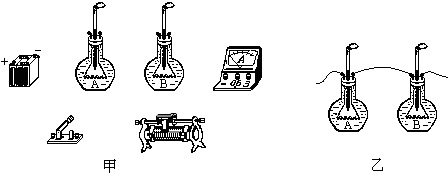
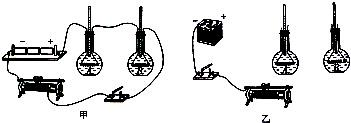 在探究电流的热效应时,甲、乙两名同学分别设计如图甲、乙所示的电路.在A、B两个完全相同的烧瓶里装有等质量的煤油,插入温度计用来显示煤油的温度.A瓶中浸泡的电阻丝的阻值大于B瓶中电阻丝的阻值.
在探究电流的热效应时,甲、乙两名同学分别设计如图甲、乙所示的电路.在A、B两个完全相同的烧瓶里装有等质量的煤油,插入温度计用来显示煤油的温度.A瓶中浸泡的电阻丝的阻值大于B瓶中电阻丝的阻值.查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:阅读理解
查看答案和解析>>
科目:初中物理 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com