
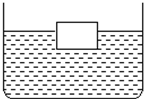
 体积为1000cm3的正方体木块,投入如图装有水的容器中,静止后木块露出水面的高度为5cm,容器的底面积为0.04m2.(g=10N/kg)
体积为1000cm3的正方体木块,投入如图装有水的容器中,静止后木块露出水面的高度为5cm,容器的底面积为0.04m2.(g=10N/kg)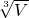 =
= =10cm=0.1m,
=10cm=0.1m,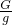 =
= =0.5kg,
=0.5kg, =
= =500kg/m3;
=500kg/m3;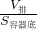 =
= =1.25×10-2m,
=1.25×10-2m,

科目:初中物理 来源: 题型:
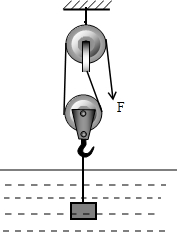 利用如如图所示的装置,把体积为1000cm3、密度为3×103kg/m3的薄石块从水面下2m处拉出水面后,再提升了5m,共用时间10s.动滑轮重为20N(不计绳子与滑轮间的摩擦,设石块的两个上升过程都是匀速)求:
利用如如图所示的装置,把体积为1000cm3、密度为3×103kg/m3的薄石块从水面下2m处拉出水面后,再提升了5m,共用时间10s.动滑轮重为20N(不计绳子与滑轮间的摩擦,设石块的两个上升过程都是匀速)求:查看答案和解析>>
科目:初中物理 来源: 题型:
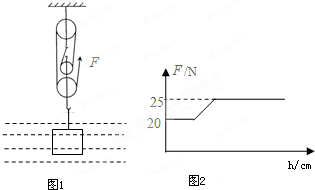 如图1所示,是用滑轮组在水中打捞文物的示意图,该均匀实心文物的密度为8×103Kg/m3,体积为1000cm3,在拉力F作用下从水中缓慢上升到岸上,拉力F的大小随文物上升的高度h的变化情况如图2所示.(g=10N/Kg)
如图1所示,是用滑轮组在水中打捞文物的示意图,该均匀实心文物的密度为8×103Kg/m3,体积为1000cm3,在拉力F作用下从水中缓慢上升到岸上,拉力F的大小随文物上升的高度h的变化情况如图2所示.(g=10N/Kg)查看答案和解析>>
科目:初中物理 来源: 题型:
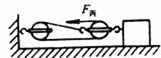 如图所示,用力F=0.5N水平拉力拉正方体木块水平匀速移动0.5m,绳子被拉动1.5m,若木块质量为750g,体积为1000cm3,(不考虑绳重及绳与轮间的摩擦),求:(g=10N/kg)
如图所示,用力F=0.5N水平拉力拉正方体木块水平匀速移动0.5m,绳子被拉动1.5m,若木块质量为750g,体积为1000cm3,(不考虑绳重及绳与轮间的摩擦),求:(g=10N/kg)查看答案和解析>>
科目:初中物理 来源: 题型:
查看答案和解析>>
科目:初中物理 来源: 题型:
 体积为1000cm3的正方体木块,投入如图装有水的容器中,静止后木块露出水面的高度为5cm,容器的底面积为0.04m2.(g=10N/kg)
体积为1000cm3的正方体木块,投入如图装有水的容器中,静止后木块露出水面的高度为5cm,容器的底面积为0.04m2.(g=10N/kg)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com