
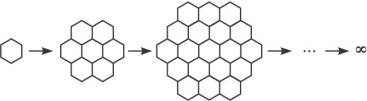
解析:本题可用两种方法求解。
解法1:极限法
碳原子数6 6+18 6+18+30+…+6n2
环数 1 1+6 1+6+12+…+3n2-3n+1
S碳=6+3×6+5×6+…+(2n-1)×6=[1+3+5+…+(2n-1)]×6=![]() ×6
×6
=6n2(n∈N)
S环=1+6+2×6+3×6+…+(n-1)×6=1+[1+2+3+…+(n-1)]×6=1+![]() ×6
×6
=3n(n-1)+1=3n2-3n+1 (n∈N)
![]()
![]() =
=![]()
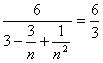 =2
=2
由此得出每个六边形所占有的碳原子数为2个。
解法2:可大胆设想将每个碳原子平均分成三等份,而每个正六边形均有6个碳原子,所以每个正六边形所占有的碳原子数为:6×![]() =2。
=2。
答案:2


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com