Question

研究CO₂与CH₄的反应使之转化为CO和H₂，对减缓燃料危机，减少温室效应具有重要的意义．
（1）已知：2CO（g）+O₂（g）═2CO₂（g）△H=-566kJ?mol^-1
2H₂（g）+O₂（g）═2H₂O（g）△H=-484kJ?mol^-1
CH₄（g）+2O₂（g）═CO₂（g）+2H₂O（g）△H=-802kJ?mol^-1
则CH₄（g）+CO₂（g）?2CO（g）+2H₂（g）△H=

 

kJ?mol^-1
（2）在密闭容器中通入物质的量浓度均为0.1mol?L^-1的CH₄与CO₂，在一定条件下发生反应CH₄（g）+CO₂（g）?2CO（g）+2H₂（g），测得CH₄的平衡转化率与温度、压强的关系如图1所示．据图可知，P₁、P₂、P₃、P₄ 由大到小的顺序

 

．在压强为P₄、1100℃的条件下，该反应5min时达到平衡点X，则用CO表示该反应的速率为

 

．该温度下，反应的平衡常数为

 

．

（3）CO和H₂在工业上还可以通过反应C（s）+H₂O（g）?CO（g）+H₂（g）来制取．
①在恒温恒容下，如果从反应物出发建立平衡，可认定平衡已达到的是

 

．
A．体系压强不再变化                B．H₂与CO的物质的量之比为1：1
C．混合气体的密度保持不变           D．气体平均相对分子质量为15，且保持不变
②在某密闭容器中同时投入四种物质，2min时达到平衡，测得容器中有1mol H₂O（g）、1mol CO（g）、2.2molH₂（g）和一定量的C（s），如果此时对体系加压，平衡向

 

（填“正”或“逆”）反应方向移动，第5min时达到新的平衡，请在图2中画出2～5min内容器中气体平均相对分子质量的变化曲线．

Answer 1

考点：用盖斯定律进行有关反应热的计算,化学平衡的影响因素,化学平衡状态的判断,化学平衡的计算

专题：化学反应中的能量变化,化学平衡专题

分析：（1）根据盖斯定律来解答；
（2）①由图可知，温度一定时，甲烷的转化率α（P₁）＞α（P₂）＞α（P₃）＞α（P₄），据此结合方程式判断压强对平衡移动的影响进行解答；
②由图1可知，压强为P₄、1100℃的条件下，该反应5min时达到平衡X点，是甲烷的转化率为80%，据此计算甲烷的浓度变化量，根据v=

△c

△t

计算v（CH₄），再利用速率之比等于化学计量数之比计算v（CO）；
利用三段式计算平衡时各组分的平衡浓度，代入平衡常数表达式计算该温度下的平衡常数；
（3）①可逆反应达到平衡状态时，正逆反应速率相等，各物质的浓度、百分含量不变，以及由此衍生的一些量也不发生变化，据此解答．解题时要注意，选择判断的物理量，随着反应的进行发生变化，当该物理量由变化到定值时，说明可逆反应到达平衡状态；
②根据增大压强，平衡向着气体体积减小的方向移动来分析．

解答： 解：（1）已知反应①2CO（g）+O₂（g）═2CO₂（g）△H=-566kJ?mol^-1
              ②2H₂（g）+O₂（g）═2H₂O（g）△H=-484kJ?mol^-1
              ③CH₄（g）+2O₂（g）═CO₂（g）+2H₂O（g）△H=-802kJ?mol^-1
根据盖斯定律，将③-①-②可得：
CH₄（g）+CO₂（g）?2CO（g）+2H₂（g）△H=（-802kJ?mol^-1）-（-566kJ?mol^-1）-（-484kJ?mol^-1）=+248KJ/mol，
故答案为：+248；
（2）由图可知，温度一定时，甲烷的转化率α（P₁）＞α（P₂）＞α（P₃）＞α（P₄），该反应正反应是气体体积增大的反应，增大压强平衡向逆反应进行，甲烷的转化率降低，故压强P₄＞P₃＞P₂＞P₁；
由图1可知，压强为P₄、1100℃的条件下，该反应5min时达到平衡X点，是甲烷的转化率为80%，甲烷的浓度变化量为0.1mol/L×80%=0.08mol/L，故v（CH₄）=

0.08mol/L

5min

=0.016mol/（L?min），根据速率之比等于化学计量数之比，所以v（CO）=2v（CH₄）=2×0.16mol/（L?min）=0.032mol/（L?min），
               CH₄（g）+CO₂（g）=2CO（g）+2H₂（g），
开始（mol/L）：0.1      0.1      0        0
变化（mol/L）：0.08     0.08     0.16     0.16 
平衡（mol/L）：0.02     0.02     0.16     0.16
故该温度下平衡常数k=

0.162×0.162

0.02×0.02

=1.64
故答案为故答案为：P₄＞P₃＞P₂＞P₁；0.032mol/（L?min）；1.64；
（3）①A、正反应方向是个气体体积增大的方向，故随着反应的进行，平衡之前，体系压强会增大，故一旦当体系压强不变，说明反应达平衡，故A正确；
B、CO与H₂的化学计量数为1：1，反应数值按物质的量比为1：1进行，不能说明到达平衡，故B错误；
C、混合气体的密度ρ=

m

V

，容器恒容，即V不变，随着反应的进行，混合气体的质量m增大，故ρ增大，一旦当ρ不变时，说明反应达平衡，故C正确；
D、反应混合物的总质量不变，随反应进行，反应混合物的总的物质的量增大，平均相对分子质量减小，混合气体的平均相对分子质量不发生变化，说明到达平衡，但达平衡时，平均相对分子质量不一定是15，故D错误；
故选AC；
②根据勒沙特列原理可知，增大压强，平衡向着气体体积减小的方向移动，此反应的逆反应方向是个气体体积减小的方向，故增大压强，向逆反应方向移动；
在第2min时，混合气体的平均相对分子质量即平均摩尔质量

.

M

=

m总

n总

=

18g+28g+4.4g

4.2mol

=12g/mol．
设在第2～5min期间的任何时刻，有XmolH₂被消耗，则有：
                       C（s）+H₂O（g）?CO（g）+H₂（g）
          初始量（mol）              1            1          2.2
          转变量（mol）                X            X          X
          剩余量（mol）             （1+X）         （1-X）      （2.2-X）
混合气体的平均相对分子质量即平均摩尔质量

.

M

=

m总

n总

=

18(1+X)+28(1-X)+2(2.2-X)

(1+X)+(1-X)+(2.2-X)

=12，故可知在2～5min期间的任意时刻，混合气体的平均相对分子质量不变，一直是12，故可得2～5min内容器中气体平均相对分子质量的变化曲线为，
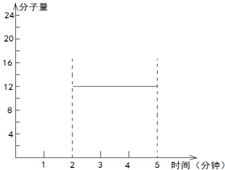
故答案为：．

点评：本题综合考查了盖斯定律的有关计算、平衡的移动以及化学平衡常数的计算等问题，综合性较强，难度较大．