Question

自然界中细菌无处不在，有些细菌的大量繁殖会导致疾病。在营养和生存空间没有限制的情况下某种细菌每20 min就繁殖一代。

（1）填写下表，计算1个细菌在不同时间（单位：min）产生后代的数量。

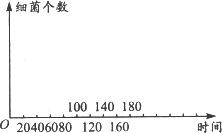
（2）能否将上述生物学问题用数学语言来表达？完成下列坐标图，绘制细菌种群的增长曲线，体会用数学模型揭示生物学现象。

（3）n代细菌的数量是多少？请用另一种数学语言——数学公式来表示。

（4）比较两类数学模型的特点。想一想，在学过的生物学内容中还有哪些生物学问题可以用数学模型来表示？总结建立数学模型的一般步骤。

Answer 1

答案：
解析：

［答案］（1） 　　（2） 　　（3）2n 　　（4）数学模型的表现形式可以是曲线图、公式等，与数学方程式相比，曲线图能更直观地反映种群数量的增长趋势，但表示的数学模型不够精确。酶的催化效率与底物的浓度、酶的浓度及反应时间等都可用曲线图来表示，光合作用、呼吸作用等生理过程也可用曲线图来表示。 　　［解析］细菌在理想状况下以几何级数增长，即第n代时，数量为2n。 　　数学模型的表现形式可以是曲线图、公式等，与数学方程式相比，曲线图能更直观地反映种群数量的增长趋势，但表示的数学模型不够精确。酶的催化效率与底物的浓度、酶的浓度及反应时间等都可用曲线图来表示，光合作用、呼吸作用等生理过程也可用曲线图来表示。