
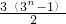
 ,进而对1或-1、
,进而对1或-1、 或-
或- 分别分析可得其可能的情况数目,由分步计数原理计算可得答案;当集合An={1,2,…,n}是解析式为y=x2的函数的值域时,其定义域中可能有的元素有±1、±
分别分析可得其可能的情况数目,由分步计数原理计算可得答案;当集合An={1,2,…,n}是解析式为y=x2的函数的值域时,其定义域中可能有的元素有±1、± 、±
、± 、±2、…±
、±2、…± ,且每对相反数至少有一个,进而对每对相反数依次分析可得其可能的情况数目,由分步计数原理计算可得an的值,即可得{an}为等比数列,再用等比数列前n和公式求出a1+a2+…+an的值.
,且每对相反数至少有一个,进而对每对相反数依次分析可得其可能的情况数目,由分步计数原理计算可得an的值,即可得{an}为等比数列,再用等比数列前n和公式求出a1+a2+…+an的值. ,且每对相反数至少有一个,
,且每对相反数至少有一个, 或-
或- ,两个中任取一个或全部都取,有3种情况;
,两个中任取一个或全部都取,有3种情况; 、±
、± 、±2、…±
、±2、…± ,且每组至少有一个,
,且每组至少有一个, 或-
或- ,两个中任取一个或全部都取,有3种情况;
,两个中任取一个或全部都取,有3种情况; 或-
或- ,两个中任取一个或全部都取,有3种情况;
,两个中任取一个或全部都取,有3种情况;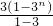 =
=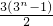 ;
;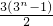 .
.

科目:高中数学 来源: 题型:
| 3(3n-1) |
| 2 |
| 3(3n-1) |
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ax3-x2+cx(a≠0)的图像如下所示,它与x轴仅有两个交点O(0,0)和A(xA,0)(xA>0).
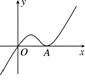
(1)证明:常数c≠0;
(2)如果xA=![]() ,求函数f(
,求函数f(![]() x)的解析式.
x)的解析式.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年北京大学附中高三(上)入学摸底数学试卷(理科)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com