
【题目】[2019·潍坊期末]某钢铁加工厂新生产一批钢管,为了了解这批产品的质量状况,检验员随机抽取了100件钢管作为样本进行检测,将它们的内径尺寸作为质量指标值,由检测结果得如下频率分布表和频率分布直方图:
分组 | 频数 | 频率 |
25.05~25.15 | 2 | 0.02 |
25.15~25.25 | ||
25.25~25.35 | 18 | |
25.35~25.45 | ||
25.45~25.55 | ||
25.55~25.65 | 10 | 0.1 |
25.65~25.75 | 3 | 0.03 |
合计 | 100 | 1 |

(1)求![]() ,
,![]() ;
;
(2)根据质量标准规定:钢管内径尺寸大于等于25.75或小于25.15为不合格,钢管尺寸在![]() 或
或![]() 为合格等级,钢管尺寸在
为合格等级,钢管尺寸在![]() 为优秀等级,钢管的检测费用为0.5元/根.
为优秀等级,钢管的检测费用为0.5元/根.
(i)若从![]() 和
和![]() 的5件样品中随机抽取2根,求至少有一根钢管为合格的概率;
的5件样品中随机抽取2根,求至少有一根钢管为合格的概率;
(ii)若这批钢管共有2000根,把样本的频率作为这批钢管的频率,有两种销售方案:
①对该批剩余钢管不再进行检测,所有钢管均以45元/根售出;
②对该批剩余钢管一一进行检测,不合格产品不销售,合格等级的钢管50元/根,优等钢管60元/根.
请你为该企业选择最好的销售方案,并说明理由.
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的准线方程为
的准线方程为![]() ,点
,点![]() 为坐标原点,不过点
为坐标原点,不过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() .
.
(1)如果直线![]() 过点
过点![]() ,求证:
,求证:![]() ;
;
(2)如果![]() ,证明:直线
,证明:直线![]() 必过一定点,并求出该定点.
必过一定点,并求出该定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某医院中随机抽取了7位医护人员的关爱患者考核分数(患者考核:10分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量
表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 98 | 88 | 96 | 91 | 90 | 92 | 96 |
| 9.9 | 8.6 | 9.5 | 9.0 | 9.1 | 9.2 | 9.8 |
(1)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到0.01);
的线性回归方程(计算结果精确到0.01);
(2)利用(1)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计某医护人员的医护专业知识考核分数为95分时,他的关爱患者考核分数(精确到0.1)
附:回归直线方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
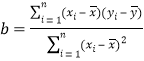 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() ,其中
,其中 ![]() .
.
(1)试讨论函数 ![]() 的单调性;
的单调性;
(2)已知当 ![]() (其中
(其中 ![]() 是自然对数的底数)时,在
是自然对数的底数)时,在 ![]() 上至少存在一点
上至少存在一点 ![]() ,使
,使 ![]() 成立,求
成立,求 ![]() 的取值范围;
的取值范围;
(3)求证:当 ![]() 时,对任意
时,对任意 ![]() ,
,![]() ,有
,有 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业招聘大学毕业生,经过综合测试,录用了14名女生和6名男生,这20名学生的测试成绩如茎叶图所示(单位:分),记成绩不小于80分者为![]() 等,小于80分者为
等,小于80分者为![]() 等.
等.

(1)求女生成绩的中位数及男生成绩的平均数;
(2)如果用分层抽样的方法从![]() 等和
等和![]() 等中共抽取5人组成“创新团队”,则从
等中共抽取5人组成“创新团队”,则从![]() 等和
等和![]() 等中分别抽几人?
等中分别抽几人?
(3)在(2)问的基础上,现从该“创新团队”中随机抽取2人,求至少有1人是![]() 等的概率.
等的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com