
 ×100%;在切割过程中的重量损耗忽略不计)
×100%;在切割过程中的重量损耗忽略不计) ×100%,即得;
×100%,即得; ×100%=
×100%= ”;
”;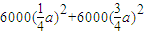 ,
,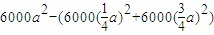 ,
,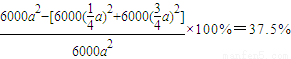 .
.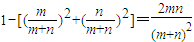 ,又
,又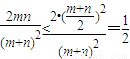 ,
,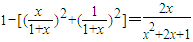 ,又x>0,∴x2+1≥2x,
,又x>0,∴x2+1≥2x,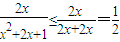 ,当且仅当x=1时等号成立.
,当且仅当x=1时等号成立.

科目:高中数学 来源: 题型:
| 原有价值-现有价值 | 原有价值 |
查看答案和解析>>
科目:高中数学 来源:2011年江苏省部分四星级高中联考高三期中数学试卷(解析版) 题型:解答题
 ×100%;在切割过程中的重量损耗忽略不计)
×100%;在切割过程中的重量损耗忽略不计)查看答案和解析>>
科目:高中数学 来源:2011年江苏省高考数学仿真押题试卷(15)(解析版) 题型:解答题
 ×100%;在切割过程中的重量损耗忽略不计)
×100%;在切割过程中的重量损耗忽略不计)查看答案和解析>>
科目:高中数学 来源:2010年江苏省南通市如皋中学高三考前指导最后一卷(解析版) 题型:解答题
 ×100%;在切割过程中的重量损耗忽略不计)
×100%;在切割过程中的重量损耗忽略不计)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com